题目内容
18.⊙O的半径为6,弦长为一元二次方程x2-5x-6=0的两根,则弦到圆心的距离及弦所对的圆心角的度数分别是( )| A. | $\sqrt{3}$和30° | B. | $\sqrt{3}$和60° | C. | 3$\sqrt{3}$和30° | D. | 3$\sqrt{3}$和60° |
分析 求出方程x2-5x-6=0的解,确定出弦AB的长,过O作OC⊥AB,连接OA,OB,如图所示,利用垂径定理得到C为AB的中点,由AB的长求出AC的长,在直角三角形AOC中,利用勾股定理求出OC的长,即为圆心O到弦AB的距离;由OA=OB=AB=6,得到三角形AOB为等边三角形,可得出∠AOB=60°,即为AB所对的圆心角的度数.
解答 解:方程x2-5x-6=0因式分解得:(x-6)(x+1)=0,
解得:x=6或x=-1(舍去),
∴AB=6,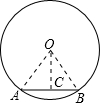
过O作OC⊥AB,连接OA,OB,如图所示,
可得C为AB的中点,即AC=BC=3,
在Rt△AOC中,OA=6,AC=3,
根据勾股定理得:OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=3$\sqrt{3}$,
∵OA=OB=AB=6,
∴△OAB为等边三角形,
∴∠AOB=60°,
则圆心O到弦AB的距离以及AB所对的圆心角分别为3$\sqrt{3}$和60°.
故选D.
点评 此题考查了垂径定理,勾股定理,以及一元二次方程-因式分解法,利用了数形结合的思想,熟练掌握定理是解本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
6.若|a|=$\frac{1}{5}$,|b|=5,则a÷b×$\frac{1}{b}$等于( )
| A. | $\frac{1}{125}$ | B. | ±$\frac{1}{125}$ | C. | ±$\frac{1}{5}$ | D. | -$\frac{1}{125}$或-$\frac{1}{5}$ |
13. 二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
 二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )| A. |  | B. |  | C. |  | D. |  |
3.平行四边形ABCD的四个顶点都在圆O上,那么四边形ABCD一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 以上都不对 |
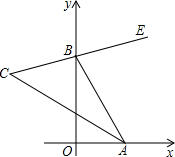 如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.
如图,在直角坐标系中,点A、B分别在射线OX、OY上移动,BE是∠ABY的角平分线,BE的反向延长线与∠OAB的平分线相交于点C,试问∠ACB的大小是否发生变化?如果保持不变,请给出证明.