题目内容
13.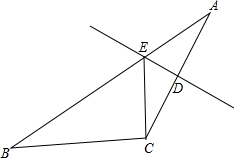 如图,△ABC中,边AC的垂直平分线分别交AB、AC于点E、D,若AE=6.
如图,△ABC中,边AC的垂直平分线分别交AB、AC于点E、D,若AE=6.(1)若AC=8,△BEC的周长为18,求△ABC的周长;
(2)若AB-BC=6,△BEC的周长为16,那么AB=11,AC=5.
分析 (1)由DE垂直平分AC,得到CE=AE=6,根据△BEC的周长为18,于是得到BE+BC+CE=BE+AE+BC=AB+BC=18,即可得到结论;
(2)由于△BEC的周长为16,得到AB+BC=16,由AB-BC=6,即可得到结果.
解答 解:(1)∵DE垂直平分AC,
∴CE=AE=6,
∵△BEC的周长为18,
∴BE+BC+CE=BE+AE+BC=AB+BC=18,
∴△ABC的周长=AB+BC+AC=18+8=26;
(2)∵△BEC的周长为16,
∴AB+BC=16,
∵AB-BC=6,
∴AB=11,BC=5,
故答案为:11,5.
点评 本题主要考查了线段垂直平分线的性质及其应用问题;应牢固掌握等腰三角形、线段垂直平分线等几何知识点的内容,并能灵活运用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.经过点(-2,1)的反比例函数图象应在( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第二、三象限 | D. | 第一、二象限 |
1.下列方程不是一元二次方程的是( )
| A. | ax+1=x2+x | B. | xy=16 | C. | x2+bx+c=0 | D. | m2=3 |
8.七年级一班课外兴趣小组准备开会讨论问题,按如下方式摆放长书桌和椅子,发现一张长书桌边可以坐6个人,加一张长书桌时可以坐8个人,再加一张长书桌时可以坐10个人…

他们发现书桌和可坐人数数量变化有规律:(请把图表中的空格补充完整)

他们发现书桌和可坐人数数量变化有规律:(请把图表中的空格补充完整)
| 长桌张数 | 1 | 2 | 3 | 4 | … | n |
| 可坐人数 | 6 | 8 | 10 | 12 | … | 2n+4 |
3.计算$\frac{2x}{x^2-1}$-$\frac{1}{x-1}$的结果是( )
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{x+1}$ | C. | $\frac{2}{x+1}$ | D. | $\frac{2}{x-1}$ |
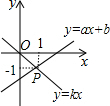 已知函数y=ax+b与函数y=kx的图象相交于点P,根据图象,可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.
已知函数y=ax+b与函数y=kx的图象相交于点P,根据图象,可得关于x、y的二元一次方程组$\left\{\begin{array}{l}{ax-y+b=0}\\{kx-y=0}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$.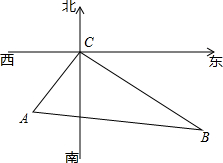 在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?
在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?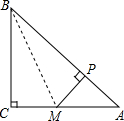 如图,∠C=90°,AM=CM,MP⊥AB于点P,求证:BP2=AP2+BC2.
如图,∠C=90°,AM=CM,MP⊥AB于点P,求证:BP2=AP2+BC2. 已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为27$\sqrt{3}$,则⊙O的半径为6.
已知正六边形ABCDEF内接于⊙O,图中阴影部分的面积为27$\sqrt{3}$,则⊙O的半径为6.