题目内容
5.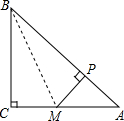 如图,∠C=90°,AM=CM,MP⊥AB于点P,求证:BP2=AP2+BC2.
如图,∠C=90°,AM=CM,MP⊥AB于点P,求证:BP2=AP2+BC2.
分析 在直角三角形中,利用勾股定理得到AB2-AC2+(AM2-MP2)=BC2+(MC2-MP2)①,AM2-MP2=AP2②,MC2+BC2-MP2=BM2-MP2=BP2③.把②③代入①证得结论.
解答 证明:∵△ABC是直角三角形,∠C=90°,
∴AB2=BC2+AC2,则AB2-AC2=BC2.
又∵在直角△AMP中,AP2=AM2-MP2,
∴AB2-AC2+(AM2-MP2)=BC2+(AM2-MP2).
又∵AM=CM,
∴AB2-AC2+(AM2-MP2)=BC2+(MC2-MP2),①
∵△APM是直角三角形,∴AM2=AP2+MP2,则AM2-MP2=AP2,②
∵△BPM与△BCM都是直角三角形,
∴BM2=BP2+MP2=MC2+BC2,
MC2+BC2-MP2=BM2-MP2=BP2,③
把②③代入①,得
AB2-AC2+AP2=BP2,即BP2=AP2+BC2.
点评 本题考查了勾股定理.正确利用等量代换是解题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.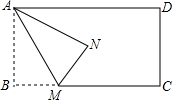 如图,一张矩形纸片ABCD中,M为BC边上一点,将△ABM沿着AM翻折,使点B落在N处,点N恰好是矩形ABCD的对角线交点,若AB=m,BC=n,则$\frac{m}{n}$为( )
如图,一张矩形纸片ABCD中,M为BC边上一点,将△ABM沿着AM翻折,使点B落在N处,点N恰好是矩形ABCD的对角线交点,若AB=m,BC=n,则$\frac{m}{n}$为( )
 如图,一张矩形纸片ABCD中,M为BC边上一点,将△ABM沿着AM翻折,使点B落在N处,点N恰好是矩形ABCD的对角线交点,若AB=m,BC=n,则$\frac{m}{n}$为( )
如图,一张矩形纸片ABCD中,M为BC边上一点,将△ABM沿着AM翻折,使点B落在N处,点N恰好是矩形ABCD的对角线交点,若AB=m,BC=n,则$\frac{m}{n}$为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
10. 如图,若∠1=∠2=∠3,则图中相似的三角形有( )
如图,若∠1=∠2=∠3,则图中相似的三角形有( )
 如图,若∠1=∠2=∠3,则图中相似的三角形有( )
如图,若∠1=∠2=∠3,则图中相似的三角形有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
14.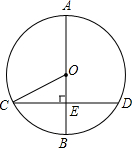 如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
 如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )
如图,⊙O的直径AB长为10,弦CD的长为8,CD⊥AB于点E,则tan∠OCE=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
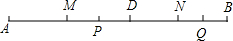 如图,D是线段AB上一点,M是AD的中点,N是DB的中点,P是MD的中点,Q是NB的中点,已知线段PQ=10,DQ=6,求线段AB的长.
如图,D是线段AB上一点,M是AD的中点,N是DB的中点,P是MD的中点,Q是NB的中点,已知线段PQ=10,DQ=6,求线段AB的长.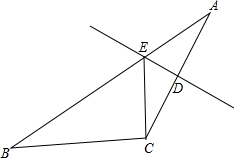 如图,△ABC中,边AC的垂直平分线分别交AB、AC于点E、D,若AE=6.
如图,△ABC中,边AC的垂直平分线分别交AB、AC于点E、D,若AE=6.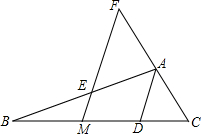 已知在△ABC中,AD平分∠BAC,MF∥AD交AB于点E,交BC于点M,求证:$\frac{BE}{CF}=\frac{BM}{CM}$.
已知在△ABC中,AD平分∠BAC,MF∥AD交AB于点E,交BC于点M,求证:$\frac{BE}{CF}=\frac{BM}{CM}$.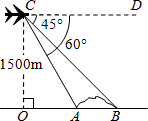 如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500米高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°,则隧道AB的长为(1500-500$\sqrt{3}$)米(结果保留根号).
如图,某高速公路建设中需要确定隧道AB的长度,已知在离地面1500米高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°,则隧道AB的长为(1500-500$\sqrt{3}$)米(结果保留根号).