题目内容
18.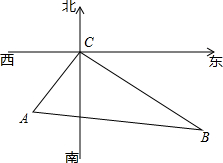 在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?
在寻找马航MH370航班过程中,A、B两艘舰艇分别沿东北方向和西北方向航行,两艘搜救舰艇接到命令后同时出发,A舰艇的速度为24海里/时,B舰艇的速度为32海里/时,经过2小时,它们同时到达事故发生的地点C,求A、B两艘舰艇在出发时相距多远?
分析 由题意得出∠ACB=90°,AC=48海里,BC=64海里,再由勾股定理求出AB即可.
解答 解:根据题意得:∠ACB=90°,AC=24×2=48(海里),BC=2×32=64(海里),
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{4{8}^{2}+6{4}^{2}}$=80(海里),
即A、B两艘舰艇在出发时相距80海里.
点评 本题考查了勾股定理的应用;熟练掌握勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
6.下面哪一个运算结果是相等的( )
| A. | ($\frac{2}{3}$)2与$\frac{{2}^{2}}{3}$ | B. | -22与(-2)2 | C. | -(-1)2011与(-1)2010 | D. | (-5)2与-52 |
10. 如图,若∠1=∠2=∠3,则图中相似的三角形有( )
如图,若∠1=∠2=∠3,则图中相似的三角形有( )
 如图,若∠1=∠2=∠3,则图中相似的三角形有( )
如图,若∠1=∠2=∠3,则图中相似的三角形有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
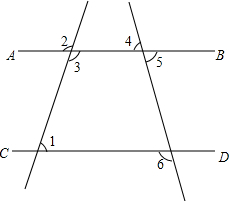 已知|3m-2n+60|与(7m-3n-60)2互为相反数,且m、n的值分别是图中∠1与∠2的度数,如果∠4=70°,试求∠6的度数.
已知|3m-2n+60|与(7m-3n-60)2互为相反数,且m、n的值分别是图中∠1与∠2的度数,如果∠4=70°,试求∠6的度数.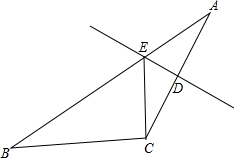 如图,△ABC中,边AC的垂直平分线分别交AB、AC于点E、D,若AE=6.
如图,△ABC中,边AC的垂直平分线分别交AB、AC于点E、D,若AE=6. 在半径为0.5米的圆柱形油罐内装入一些油,截面如图所示,若油面宽AB=0.6米,则油的最大深度是0.1米.
在半径为0.5米的圆柱形油罐内装入一些油,截面如图所示,若油面宽AB=0.6米,则油的最大深度是0.1米.