题目内容
6.为保护学生的身体健康,某中学课桌椅的高度都是按一定的关系配套设计的,下表列出5套符合条件的课桌椅的高度:| 椅子高度x(cm) | 45 | 42 | 39 | 36 | 33 |
| 桌子高度y(cm) | 84 | 79 | 74 | 69 | 64 |
(2)现有一把高38cm的椅子和一张高72.2cm的课桌,它们是否配套?为什么?
分析 (1)设经过点(45,84),(42,79)的一次函数解析式为y=kx+b,代入得出$\left\{\begin{array}{l}{45k+b=84}\\{42k+b=79}\end{array}\right.$,求出k、b的值,得出解析式,再判断由表中剩下的各个点是否在函数解析式上,即可得出答案;
(2)把(38,72.2)代入y=$\frac{5}{3}$x+9,看看左边和右边是否相等即可.
解答 解:(1)设经过点(45,84),(42,79)的一次函数解析式为y=kx+b,
代入得:$\left\{\begin{array}{l}{45k+b=84}\\{42k+b=79}\end{array}\right.$,
解得:k=$\frac{5}{3}$,b=9,
即y=$\frac{5}{3}$x+9,
把点(39,74)、(36,69),(33,64)代入y=$\frac{5}{3}$x+9,左边都等于右边,
即点都在直线y=-$\frac{5}{3}$x+159上,
所以y与x的函数关系式是y=$\frac{5}{3}$x+9;
(2)一把高38cm的椅子和一张高72.2cm的课桌,它们配套,
理由是:∵把(38,72.2)代入y=$\frac{5}{3}$x+9得:左边=右边,
∴一把高38cm的椅子和一张高72.2cm的课桌,它们配套.
点评 本题考查了用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征的应用,能求出函数解析式是解此题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
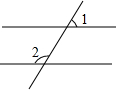 如图,已知直线AB∥CD,若∠1=2x°,∠2=(3x+30)°,则∠1=60度.
如图,已知直线AB∥CD,若∠1=2x°,∠2=(3x+30)°,则∠1=60度.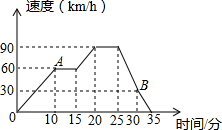 如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题:
如图是一辆汽车的速度随时间变化而变化的图象,回答下面的问题: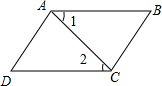 如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠B=∠D;④∠D=∠ACB,其中正确的有①②③.
如图,已知∠1=∠2,∠BAD=∠BCD,则下列结论:①AB∥CD;②AD∥BC;③∠B=∠D;④∠D=∠ACB,其中正确的有①②③. 如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.
如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.