题目内容
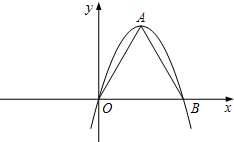 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.(1)“抛物线三角形”一定是
(2)若抛物线y=-x2+bx(b>0)的“抛物线三角形”是等腰直角三角形,求b的值;
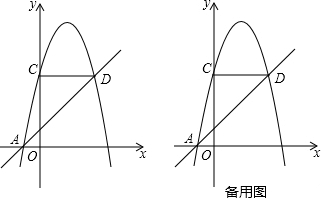
(3)如图,△OAB是抛物线y=-x2+b′x(b′>0)的“抛物线三角形”,是否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由.
(4)若抛物线y=-x2+4mx-8m+4与直线y=3交点的横坐标均为整数,是否存在整数m的值使这条抛物线的“抛物线三角形”有一边上的中线长恰好等于这边的长?若存在,直接写出m的值;若不存在,说明理由.
考点:二次函数综合题
专题:
分析:(1)抛物线的顶点必在抛物线与x轴两交点连线的垂直平分线上,因此这个“抛物线三角形”一定是等腰三角形.
(2)观察抛物线的解析式,它的开口向下且经过原点,由于b>0,那么其顶点在第一象限,而这个“抛物线三角形”是等腰直角三角形,必须满足顶点坐标的横、纵坐标相等,以此作为等量关系来列方程解出b的值.
(3)由于矩形的对角线相等且互相平分,所以若存在以原点O为对称中心的矩形ABCD,那么必须满足OA=OB,结合(1)的结论,这个“抛物线三角形”必须是等边三角形,首先用b′表示出AE、OE的长,通过△OAB这个等边三角形来列等量关系求出b′的值,进而确定A、B的坐标,即可确定C、D的坐标,利用待定系数即可求出过O、C、D的抛物线的解析式.
(4)联立两个函数的解析式,通过所得方程先求出这个方程的两个根,然后通过这两个根都是整数确定m的整数值.
(2)观察抛物线的解析式,它的开口向下且经过原点,由于b>0,那么其顶点在第一象限,而这个“抛物线三角形”是等腰直角三角形,必须满足顶点坐标的横、纵坐标相等,以此作为等量关系来列方程解出b的值.
(3)由于矩形的对角线相等且互相平分,所以若存在以原点O为对称中心的矩形ABCD,那么必须满足OA=OB,结合(1)的结论,这个“抛物线三角形”必须是等边三角形,首先用b′表示出AE、OE的长,通过△OAB这个等边三角形来列等量关系求出b′的值,进而确定A、B的坐标,即可确定C、D的坐标,利用待定系数即可求出过O、C、D的抛物线的解析式.
(4)联立两个函数的解析式,通过所得方程先求出这个方程的两个根,然后通过这两个根都是整数确定m的整数值.
解答:解:(1)如图;
根据抛物线的对称性,抛物线的顶点A必在O、B的垂直平分线上,所以OA=AB,即:“抛物线三角形”必为等腰三角形.
故答案为:等腰.
(2)当抛物线y=-x2+bx(b>0)的“抛物线三角形”是等腰直角三角形,
该抛物线的顶点(
,
),满足
=
(b>0).
则b=2.
(3)存在.
如图,作△OCD与△OAB关于原点O中心对称,则四边形ABCD为平行四边形.
当OA=OB时,平行四边形ABCD是矩形,
又∵AO=AB,
∴△OAB为等边三角形.
∴∠AOB=60°,
作AE⊥OB,垂足为E,
∴AE=OEtan∠AOB=
OE.
∴
=
×
(b>0).
∴b′=2
.
∴A(
,3),B(2
,0).
∴C(-
,-3),D(-2
,0).
设过点O、C、D的抛物线为y=mx2+nx,则
,
解得
,
故所求抛物线的表达式为y=x2+2
x.
(4)由-x2+4mx-8m+4=3,x=
=2m±
,
当x为整数时,须 4m2-8m+1为完全平方数,设 4m2-8m+1=n2 (n是整数)整理得:
(2m-2)2-n2=3,即 (2m-2+n)(2m-2-n)=3
两个整数的积为7,∴
或
或
或
解得:
或
或
或
,
综上,得:m=2或m=0;
∴抛物线与直线y=3交点的横坐标均为整数时m=2或m=0.
根据抛物线的对称性,抛物线的顶点A必在O、B的垂直平分线上,所以OA=AB,即:“抛物线三角形”必为等腰三角形.
故答案为:等腰.
(2)当抛物线y=-x2+bx(b>0)的“抛物线三角形”是等腰直角三角形,
该抛物线的顶点(
| b |
| 2 |
| b2 |
| 4 |
| b |
| 2 |
| b2 |
| 4 |
则b=2.
(3)存在.

如图,作△OCD与△OAB关于原点O中心对称,则四边形ABCD为平行四边形.
当OA=OB时,平行四边形ABCD是矩形,
又∵AO=AB,
∴△OAB为等边三角形.
∴∠AOB=60°,
作AE⊥OB,垂足为E,
∴AE=OEtan∠AOB=
| 3 |
∴
| b′2 |
| 4 |
| 3 |
| b′ |
| 2 |
∴b′=2
| 3 |
∴A(
| 3 |
| 3 |
∴C(-
| 3 |
| 3 |
设过点O、C、D的抛物线为y=mx2+nx,则
|
解得
|
故所求抛物线的表达式为y=x2+2
| 3 |
(4)由-x2+4mx-8m+4=3,x=
4m±
| ||
| 2 |
| 4m2-8m+1 |
当x为整数时,须 4m2-8m+1为完全平方数,设 4m2-8m+1=n2 (n是整数)整理得:
(2m-2)2-n2=3,即 (2m-2+n)(2m-2-n)=3
两个整数的积为7,∴
|
|
|
|
解得:
|
|
|
|
综上,得:m=2或m=0;
∴抛物线与直线y=3交点的横坐标均为整数时m=2或m=0.
点评:本二次函数综合题融入了新定义的形式,涉及到:二次函数的性质及解析式的确定、等腰三角形的判定和性质、矩形的判定和性质等知识,重在考查基础知识的掌握情况,解题的思路并不复杂,但计算过程较为复杂,间接增大了题目的难度.

练习册系列答案
相关题目
已知式子3x2-4x+6的值为9,则3x2-4x-2的值为( )
| A、1 | B、0 | C、7 | D、-7 |
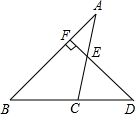 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=30°,∠D=55°,求∠ACD的度数.
如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=30°,∠D=55°,求∠ACD的度数.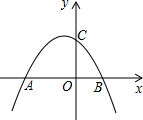 如图,抛物线y=-
如图,抛物线y=-