题目内容
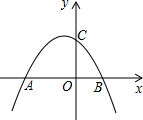 如图,抛物线y=-
如图,抛物线y=-| 3 |
| 8 |
| 3 |
| 4 |
(1)求点A、B的坐标;
(2)设D为y轴上的一点,当△ACD的面积等于△ACB的面积时,求D点的坐标;
(3)已知:直线y=-
| k |
| 4 |
考点:二次函数综合题
专题:
分析:(1)当y=0时,求出x即可.
(2)利用平行线间的高相等,过B点作直线L1∥AC交y轴于点D1,可得出S△ACB=S△ACD1,利用坐标求出直线AC解析式,再求出直线L1的表达式,即可求出D1坐标,再根据根据关于对称性可求得D2坐标.
(3)以AB为直径作⊙F,过E点作⊙F的切线,切点为H,利用待定系数法求出切线的解析式,要使以A、B、M为顶点所作的直角三角形有且只有四个,就要使直线y=-
x+k(k>0)与⊙F相交,即可求出k的范围.
(2)利用平行线间的高相等,过B点作直线L1∥AC交y轴于点D1,可得出S△ACB=S△ACD1,利用坐标求出直线AC解析式,再求出直线L1的表达式,即可求出D1坐标,再根据根据关于对称性可求得D2坐标.
(3)以AB为直径作⊙F,过E点作⊙F的切线,切点为H,利用待定系数法求出切线的解析式,要使以A、B、M为顶点所作的直角三角形有且只有四个,就要使直线y=-
| k |
| 4 |
解答:解:(1)令y=0,-
x2-
x+3=0,
解得x1=-4,x2=2,
∴点A、B的坐标分别为A(-4,0)、B(2,0).
(2)如图1,过B点作直线L1∥AC交y轴于点D1,则S△ACB=S△ACD1,
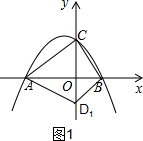
设直线AC的表达式为y=kx+b,代入A(-4,0),C(0,3),
得
,解得
,
∴直线AC表达式y=
x+3.
∵直线L1平行于AC,
∴设直线L1的表达式为y=
x+b,代入B(2,0).
解得:b=-
,
∴D1点的坐标是(0,-
),
根据关于对称性可求得D2坐标为(0,
),
∴D点的坐标分别为:(0,-
),(0,
)
(3)∵直线y=-
x+k(k>0)交x轴于点E,令y=0,则-
x+k=0,解得x=4,
∴E点坐标为(4,0),
如图2,以AB为直径作⊙F,过E点作⊙F的切线,切点为H,这样的直线有2条,
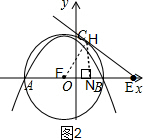
∵直线y=-
x+k(k>0)中的k>0,
∴只取x轴上方的一条切线.
连接FH,过H作HN⊥x轴于点N.
∵A(-4,0),B(2,0),
∴F(-1,0),
∴FE=5,⊙F半径FH=FB=3.
在Rt△HEF中,
HE=
=4,sin∠HFE=
,cos∠HFE=
.
在Rt△FHN中,HN=HN•sin∠HFE=3×
=
,
FN=HN•cos∠HFE=3×
=
,则ON=
,
∴H点坐标为(
,
)
设直线HE的表达式为y=kx+b,代入H(
,
),E(4,0),则有
,解得
,
所以切线HE的表达式为y=-
x+3.
∵过A、B点作x轴的垂线,其与直线y=-
x+3的两个交点均可以与A、B点构成直角三角形,
∴要使以A、B、M为顶点所作的直角三角形有且只有四个,就要使直线y=-
x+k(k>0)与⊙F相交,
∵过E点的直线y=-
x+3与⊙F相切时,直线与y轴的交点坐标是(0,3),
∴过E点的直线y=-
x+k(k>0)与⊙F相交时k的范围是0<k<3.
| 3 |
| 8 |
| 3 |
| 4 |
解得x1=-4,x2=2,
∴点A、B的坐标分别为A(-4,0)、B(2,0).
(2)如图1,过B点作直线L1∥AC交y轴于点D1,则S△ACB=S△ACD1,

设直线AC的表达式为y=kx+b,代入A(-4,0),C(0,3),
得
|
|
∴直线AC表达式y=
| 3 |
| 4 |
∵直线L1平行于AC,
∴设直线L1的表达式为y=
| 3 |
| 4 |
解得:b=-
| 3 |
| 2 |
∴D1点的坐标是(0,-
| 3 |
| 2 |
根据关于对称性可求得D2坐标为(0,
| 15 |
| 2 |
∴D点的坐标分别为:(0,-
| 3 |
| 2 |
| 15 |
| 2 |
(3)∵直线y=-
| k |
| 4 |
| k |
| 4 |
∴E点坐标为(4,0),
如图2,以AB为直径作⊙F,过E点作⊙F的切线,切点为H,这样的直线有2条,

∵直线y=-
| k |
| 4 |
∴只取x轴上方的一条切线.
连接FH,过H作HN⊥x轴于点N.
∵A(-4,0),B(2,0),
∴F(-1,0),
∴FE=5,⊙F半径FH=FB=3.
在Rt△HEF中,
HE=
| 52-32 |
| 4 |
| 5 |
| 3 |
| 5 |
在Rt△FHN中,HN=HN•sin∠HFE=3×
| 4 |
| 5 |
| 12 |
| 5 |
FN=HN•cos∠HFE=3×
| 3 |
| 5 |
| 9 |
| 5 |
| 4 |
| 5 |
∴H点坐标为(
| 4 |
| 5 |
| 12 |
| 5 |
设直线HE的表达式为y=kx+b,代入H(
| 4 |
| 5 |
| 12 |
| 5 |
|
|
所以切线HE的表达式为y=-
| 3 |
| 4 |
∵过A、B点作x轴的垂线,其与直线y=-
| 3 |
| 4 |
∴要使以A、B、M为顶点所作的直角三角形有且只有四个,就要使直线y=-
| k |
| 4 |
∵过E点的直线y=-
| 3 |
| 4 |
∴过E点的直线y=-
| k |
| 4 |
点评:本题主要考查了二次函数综合题,解题的关键是明确直线y=-
x+k(k>0)与⊙F相交时,以A、B、M为顶点所作的直角三角形有且只有四个.据此求出k的取值范围.
| k |
| 4 |

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
如果a的相反数是-3,那么a的值是( )
| A、-3 | B、3或-3 | C、3 | D、0 |
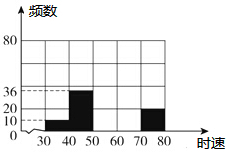
 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.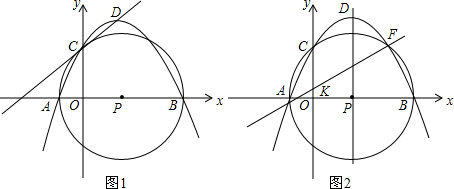
 理,得到不完整的图表:
理,得到不完整的图表: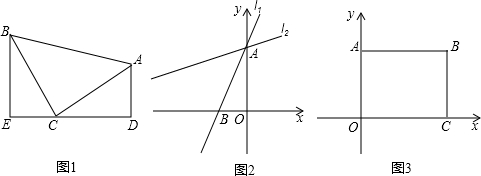
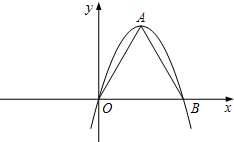
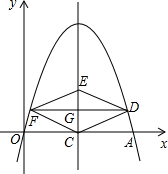 如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.
如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.