题目内容
如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有x1+x2=-
,x1x2=
.这是一元二次方程根与系数的关系,我们可以用它来解题:设x1,x2是方程x2+6x-3=0的两根,求x12+x22的值.解法可以这样:∵x1+x2=-6,x1x2=-3,则x12+x22=(x1+x2)2-2x1x2=(-6)2-2×(-3)=42.
请根据以上解法解答下题:已知x1,x2是方程x2-4x+2=0的两根,求:
(1)
+
的值;
(2)x1-x2的值.
| b |
| a |
| c |
| a |
请根据以上解法解答下题:已知x1,x2是方程x2-4x+2=0的两根,求:
(1)
| 1 |
| x1 |
| 1 |
| x2 |
(2)x1-x2的值.
考点:根与系数的关系
专题:阅读型
分析:先由根与系数的关系得出x1+x2=4,x1•x2=2,再把所求代数式变形为两根之积或两根之和的形式,然后代入数值计算即可.
解答:解:∵x1,x2是方程x2-4x+2=0的两根,
∴x1+x2=4,x1•x2=2.
(1)∵
+
=
,
∴
+
=
=2;
(2)∵(x1-x2)2=(x1+x2)2-4x1•x2,
∴x1-x2=±
=±
=±2
.
∴x1+x2=4,x1•x2=2.
(1)∵
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
∴
| 1 |
| x1 |
| 1 |
| x2 |
| 4 |
| 2 |
(2)∵(x1-x2)2=(x1+x2)2-4x1•x2,
∴x1-x2=±
| (x1+x2)2-4x1x2 |
| 16-8 |
| 2 |
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
学校为了了解300名初一学生的体重情况,从中抽取30学生进行测量,下列说法中正确的是( )
| A、总体是300 |
| B、样本容量为30 |
| C、样本是30名学生 |
| D、个体是每个学生 |


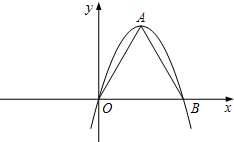 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.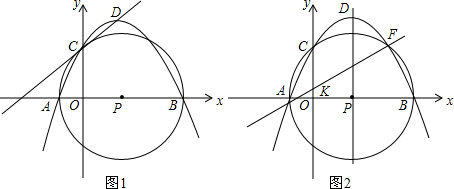
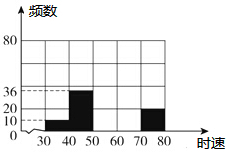 理,得到不完整的图表:
理,得到不完整的图表: 如图,已知∠GAB=∠GDF,∠FAC+∠ACE=180°,求证:∠1=∠2.
如图,已知∠GAB=∠GDF,∠FAC+∠ACE=180°,求证:∠1=∠2.