题目内容
8.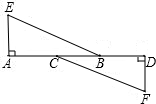 如图点A、B、C、D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A、D,AE=DF,AC=BD,求证:△EAB≌△FDC.
如图点A、B、C、D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A、D,AE=DF,AC=BD,求证:△EAB≌△FDC.
分析 利用等式的性质可得AB=CD,然后利用SAS判定△EAB≌△FDC即可.
解答 证明:∵AC=BD,
∴AC+BC=BC+BD,
即AB=CD,
∵AE⊥AD,FD⊥AD,
∴∠A=∠D=90°,
在△AEB和△DFC中$\left\{\begin{array}{l}{AE=DF}\\{∠A=∠D}\\{AB=CD}\end{array}\right.$,
∴△EAB≌△FDC(SAS).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目