题目内容
18.已知一次函数y=x-2与x轴,y轴分别交于点A和点B(1)求点A,点B的坐标,及△OAB的面积;
(2)在坐标轴上确定一点C,使△ABC是直角三角形;
(3)在坐标系中确定一点D,使点A、O、B、D四点构成的四边形为平行四边形.
分析 (1)分别将x=0、y=0代入一次函数解析式中求出与之对应的y、x的值,由此即可得出点B、A的坐标,再根据三角形的面积公式即可求出△OAB的面积;
(2)由点A、B的坐标可得出∠OAB=∠OBA=45°,分∠ACB=90°、∠BAC=90°及∠ABC=90°三种情况考虑,根据点A、B的坐标结合等腰直角三角形的性质即可得出点C的坐标,此题得解;
(3)分AB为边及AB为对角线两种情况考虑,根据点A、B、O的坐标结合平行四边形的性质即可得出点D的坐标,此题得解.
解答 解:(1)当x=0时,y=x-2=-2,
∴点B的坐标为(0,-2);
当y=x-2=0时,x=2,
∴点A的坐标为(2,0).
∴OA=OB=2,
∴S△OAB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×2×2=2.
(2)∵点A(2,0),点B(0,-2),
∴∠OAB=∠OBA=45°.
△ABC为直角三角形分三种情况(如图1所示):
当∠ACB=90°时,点C与点O重合,
∴点C的坐标为(0,0);
当∠BAC=90°时,∵△BAC为等腰直角三角形,
∴点C的坐标为(0,2);
当∠ABC=90°时,∵△ABC为等腰直角三角形,
∴点C的坐标为(-2,0).
综上所述:使△ABC为直角三角形的点C的坐标是(0,0)、(0,2)或(-2,0).
(3)点A、O、B、D四点构成的四边形为平行四边形分两种情况(如图2所示):
①当AB为边时,∵四边形ABOD或四边形ABDO为平行四边形,
∴点D的坐标为(2,2)或(-2,-2);
②当AB为对角线时,∵四边形ADBO为平行四边形,
∴点D的坐标为(2,-2).
综上所述:使点A、O、B、D四点构成的四边形为平行四边形的点D的坐标为(2,2)、(-2,-2)或(2,-2).
点评 本题考查了一次函数图象上点的坐标特征、三角形的面积、等腰直角三角形以及平行四边形的性质,解题的关键是:(1)利用一次函数图象上点的坐标特征求出点A、B的坐标;(2)分∠ACB=90°、∠BAC=90°及∠ABC=90°三种情况考虑;(3)分AB为边及AB为对角线两种情况考虑.

| A. | a>2 | B. | a≥2 | C. | a>-2 | D. | a≥-2 |
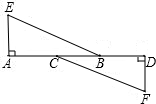 如图点A、B、C、D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A、D,AE=DF,AC=BD,求证:△EAB≌△FDC.
如图点A、B、C、D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A、D,AE=DF,AC=BD,求证:△EAB≌△FDC.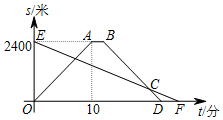 小明租用共享单车从家出发,匀速骑行到相距2 400米的邮局办事.小明出发的同时,他的爸爸以每分钟96米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
小明租用共享单车从家出发,匀速骑行到相距2 400米的邮局办事.小明出发的同时,他的爸爸以每分钟96米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.