题目内容
19.已知正比例函数y1=mx的图象与反比例函数y2=$\frac{10-m}{x}$(m为常数,m≠0)的图象有一个交点的横坐标是2.(1)求m的值;
(2)写出当y1<y2时,自变量x的取值范围.
分析 (1)把交点的横坐标代入函数解析式,列出一元一次方程,解方程即可;
(2)根据题意列出二元一次方程组,解方程组得出两个交点坐标,即可得出答案.
解答 解:(1)∵正比例函数y1=mx的图象与反比例函数y2=$\frac{10-m}{x}$(m为常数,且m≠0)的图象有一个交点的横坐标是2,
∴y1=2m,y2=$\frac{10-m}{2}$,
∵y1=y2,
∴2m=$\frac{10-m}{2}$,
解得,m=2;
(2)由(1)得:正比例函数为y1=2x,反比例函数为y2=$\frac{8}{x}$;
解方程组$\left\{\begin{array}{l}{y=2x}\\{y=\frac{8}{x}}\end{array}\right.$得:$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-4}\end{array}\right.$,
∴这两个函数图象的交点坐标为(2,4)和(-2,-4),
当y1<y2时,自变量x的取值范围为x<-2或0<x<2.
点评 本题考查的是反比例函数与一次函数的交点问题,灵活运用待定系数法求出函数解析式、掌握正比例函数与反比例函数图象的交点的求法是解题的关键.

练习册系列答案
相关题目
10.学校准备推荐一位老师参加业务技能比赛,对甲、乙两位老师进行三项测试,他们各自的成绩(百分制)如下表:
学校将课件制作、片段教学、综合素质按三项得分的2:3:5确定最终成绩,并根据成绩择优推荐,请你通过计算说明谁被推荐参加比赛?
| 选手 | 课件制作 | 片段教学 | 综合素质 |
| 甲 | 85 | 78 | 85 |
| 乙 | 73 | 80 | 82 |
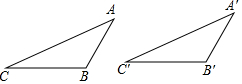 如图,∠B=∠B′>90°,AB=A′B′,AC=A′C′.求证:△ABC≌△A′B′C′.
如图,∠B=∠B′>90°,AB=A′B′,AC=A′C′.求证:△ABC≌△A′B′C′.
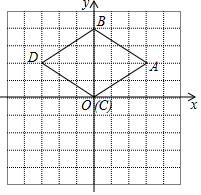 如图所示,△DBC是由△ABC经过变换得到的图形,分别写出点A、B、C、D的坐标,观察点A与点D的坐标之间的关系,如果△ABC中任一点N的坐标为N(x,y),它在△BCD中的对应点M的坐标是什么?
如图所示,△DBC是由△ABC经过变换得到的图形,分别写出点A、B、C、D的坐标,观察点A与点D的坐标之间的关系,如果△ABC中任一点N的坐标为N(x,y),它在△BCD中的对应点M的坐标是什么?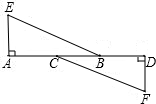 如图点A、B、C、D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A、D,AE=DF,AC=BD,求证:△EAB≌△FDC.
如图点A、B、C、D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A、D,AE=DF,AC=BD,求证:△EAB≌△FDC.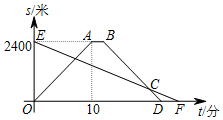 小明租用共享单车从家出发,匀速骑行到相距2 400米的邮局办事.小明出发的同时,他的爸爸以每分钟96米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
小明租用共享单车从家出发,匀速骑行到相距2 400米的邮局办事.小明出发的同时,他的爸爸以每分钟96米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.