题目内容
10.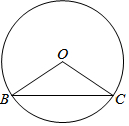 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.(1)求∠BOC的度数.
(2)若⊙O的半径为4,求弦BC和劣弧BC组成的弓形面积.
分析 (1)根据圆周角定理即可得出结论;
(2)过O作OD⊥BC于D,根据扇形的面积和三角形的面积公式即可得到结论.
解答 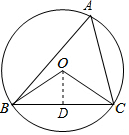 解:(1)如图,∵∠BOC=2∠A,∠BOC+∠A=180°,
解:(1)如图,∵∠BOC=2∠A,∠BOC+∠A=180°,
∴∠BOC=120°;
(2)过O作OD⊥BC于D,
∵∠BOC=120°,
∴∠BOD=60°,
∵BO=4,
∴OD=2,BD=2$\sqrt{3}$,
∴BC=4$\sqrt{3}$,
∴弦BC和劣弧BC组成的弓形面积=S扇形BOC-S△BOC=$\frac{120•π×{4}^{2}}{360}$-$\frac{1}{2}$×4$\sqrt{3}$×2=$\frac{16π}{3}$-4$\sqrt{3}$.
点评 本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
20.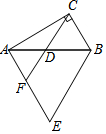 如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
 如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
5.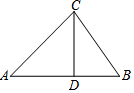 如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )
如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )
 如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )
如图,在△ABC中,CD⊥AB于点D,己知AC=a,∠A=α,∠B=β,则BD的长是( )| A. | $\frac{a•sinα}{tanβ}$ | B. | $\frac{a•cosα}{tanβ}$ | C. | a•sinα•tanβ | D. | a•cosα•tanβ |
2.下列计算正确的是( )
| A. | 6-(-6)=0 | B. | (-2.8)+1.2=1.6 | C. | (+2)+(-5)=-3 | D. | $\frac{1}{3}-({-\frac{2}{3}})=-\frac{1}{3}$ |
20.已知二次函数y=-(x-h)2+1(为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最大值为-5,则h的值为( )
| A. | 3-$\sqrt{6}$或1+$\sqrt{6}$ | B. | 3-$\sqrt{6}$或3+$\sqrt{6}$ | C. | 3+$\sqrt{6}$或1-$\sqrt{6}$ | D. | 1-$\sqrt{6}$或1+$\sqrt{6}$ |
 一个长方形的周长是12 cm,一边长是x( cm).
一个长方形的周长是12 cm,一边长是x( cm).