题目内容
20.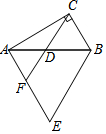 如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )
如图,在△ABC中,∠ACB=90°,∠CBA=60°.△ABE是等边三角形,D是AB的中点,连接CD并延长,交AE于点F.若CD=2,则EF的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | $\frac{3}{2}$ |
分析 根据直角三角形的性质得到△CDB是等边三角形,得到DF∥BE,根据三角形中位线定理计算即可.
解答 解:∵∠ACB=90°,∠CBA=60°,
∴∠ABC=30°,
∴AB=2CD=4,
∵∠ACB=90°,D是AB的中点,
∴CD=BD,又∠CBA=60°,
∴△CDB是等边三角形,
∵△ABE是等边三角形,
∴DF∥BE,
∴EF=$\frac{1}{2}$AE=2,
故选:B.
点评 本题考查的是直角三角形的性质、等边三角形的性质,掌握直角三角形中,30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
15.若a<b,则下列不等式成立的是( )
| A. | ma<mb | B. | 2a>2b | C. | -2a>-2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
12.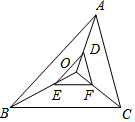 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
 如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )
如图,在O为△ABC内一点,D,E,F分别是OA,OB,OC上的点,且$\frac{OD}{AD}$=$\frac{OE}{BE}$=$\frac{OF}{CF}$=$\frac{1}{2}$,则$\frac{EF}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
9.一个三角形三个内角的度数之比为3:4:5,这个三角形一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
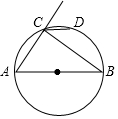 如图,AB为⊙O的直径,AB=10,弦AC=6,∠ACB的外角平分线交⊙O于点D,求CD的长.
如图,AB为⊙O的直径,AB=10,弦AC=6,∠ACB的外角平分线交⊙O于点D,求CD的长. 如图,某数学兴趣小组将一段长为4的铁丝,围成以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形的最大面积为1.
如图,某数学兴趣小组将一段长为4的铁丝,围成以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形的最大面积为1.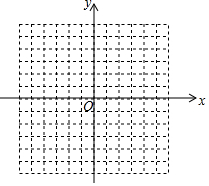 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,-3),B(5,-1),C(-1,3),结合所给的平面直角坐标系,解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点(即这些小正方形的顶点)上,且它们的坐标分别是A(2,-3),B(5,-1),C(-1,3),结合所给的平面直角坐标系,解答下列问题: 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.