题目内容
18.例:∵$\frac{1}{n(n+1)(n+2)}=\frac{1}{2}[\frac{1}{n(+1)}-\frac{1}{(n+1)(n+2)}]$∴$\frac{1}{1×2×3}+\frac{1}{2×3×4}+\frac{1}{3×4×5}+…+$$\frac{1}{n×(n+1)(n+2)}$
=$\frac{1}{2}(\frac{1}{1×2}-\frac{1}{2×3}+\frac{1}{2×3}-\frac{1}{3×4}+…+\frac{1}{n(n+1)}$$-\frac{1}{(n+1)(n+2)})$
=$\frac{1}{2}(\frac{1}{1×2}-\frac{1}{(n+1)(n+2)})=\frac{{n}^{2}+3n}{4(n+1)(n+2)}$
认真领悟上例的解法原理,并根据原理求下列式子的值.
(1)$\frac{1}{1×3×5}+\frac{1}{3×5×7}+\frac{1}{5×7×9}+\frac{1}{7×9×11}$
(2)$\frac{1}{1×3×5}+\frac{1}{3×5×7}+\frac{1}{5×7×9}+…+$$\frac{1}{n(n+2)(n+4)}$.
分析 (1)根据题目中的例子可以解答本题;
(2)根据(1)中的解答可以解答本题.
解答 解:(1)$\frac{1}{1×3×5}+\frac{1}{3×5×7}+\frac{1}{5×7×9}+\frac{1}{7×9×11}$
=$\frac{1}{4}(\frac{1}{1×3}-\frac{1}{3×5}+\frac{1}{3×5}-\frac{1}{5×7}+\frac{1}{5×7}-\frac{1}{7×9}+\frac{1}{7×9}-\frac{1}{9×11})$
=$\frac{1}{4}×(\frac{1}{3}-\frac{1}{99})$
=$\frac{8}{99}$;
(2)$\frac{1}{1×3×5}+\frac{1}{3×5×7}+\frac{1}{5×7×9}+…+$$\frac{1}{n(n+2)(n+4)}$
=$\frac{1}{4}(\frac{1}{1×3}-\frac{1}{3×5}+\frac{1}{3×5}-\frac{1}{5×7}+…+\frac{1}{n(n+2)}-\frac{1}{(n+2)(n+4)})$
=$\frac{1}{4}×(\frac{1}{3}-\frac{1}{(n+2)(n+4)})$
=$\frac{{n}^{2}+6n+5}{12(n+2)(n+4)}$.
点评 本题考查分式的混合运算,解答本题的关键是明确题意,找出所求问题需要的条件,明确分式混合运算的计算方法.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
9.一个三角形三个内角的度数之比为3:4:5,这个三角形一定是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
13.已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2009的值为( )
| A. | (-3)2009 | B. | -1 | C. | 0 | D. | 1 |
3.己知△ABC中,∠C=Rt∠,若AC=$\sqrt{3}$,BC=1,则sinA的值是( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
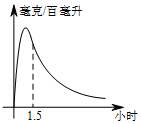 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示,1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示)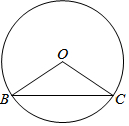 在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.
在⊙O中,己知弦BC所对的圆周角∠BAC与圆心角∠BOC互补.