题目内容
3. 如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )
如图,A,B是数轴上两点,过点B作BC⊥x轴,若BC=2,以A为圆心,AC为半径作圆弧交数轴于点P,若点P所表示的数是$\sqrt{13}$-2,则点A表示的数是( )| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
分析 首先在直角三角形中,利用勾股定理可以求出线段CA的长度,然后根据AC=AP即可求出AP的长度,接着可以求出数轴上点A所表示的数.
解答 解:∵在Rt△ABC中,CA=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴AC=AP=$\sqrt{13}$,
∵点P所表示的数是$\sqrt{13}$-2,
∴点P所表示的数是$\sqrt{13}$-2-$\sqrt{13}$=-2.
故选:B.
点评 此题主要考查了实数与数轴之间的对应关系,首先正确根据数在数轴上的位置判断数的符号以及绝对值的大小,再根据运算法则进行判断.

练习册系列答案
相关题目
13.下列事件为必然事件的是( )
| A. | 明天怀柔区必然下雪 | |
| B. | 本次期末数学考试每个考场都只有一名考生 | |
| C. | 百米短跑比赛,一定产生第一名 | |
| D. | 每天天安门的升旗时间都是上午10点 |
14.下列命题:①过三角形的一个顶点作对边的垂线叫做三角形的高;②三角形的外角大于它的任何一个内角;③直角三角形有两条高和边重合;④三角形的角平分线、中线、高都在三角形的内部.其中假命题的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.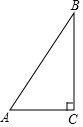 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{3\sqrt{3}}{4}$ |
18.某景点的门票价格如下表:
某校八年级(一)、(二)两班共102人去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元,则一共支付1118元,如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?
| 购票人数 | 1~50 | 51~100 | 100以上 |
| 每人门票价 | 12 | 10 | 8 |
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?
8. 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若AB=m,CD=n,则△ABD的面积等于( )
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若AB=m,CD=n,则△ABD的面积等于( )
 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若AB=m,CD=n,则△ABD的面积等于( )
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若AB=m,CD=n,则△ABD的面积等于( )| A. | mn | B. | $\frac{1}{2}$mn | C. | 2mn | D. | $\frac{1}{3}$mn |
15.方程x(x-1)=6的解是( )
| A. | x=-2 | B. | x=3 | C. | x1=-2,x2=3 | D. | x1=2,x2=-3 |
1. 如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )
如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )
 如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )
如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )| A. | 75° | B. | 90° | C. | 120° | D. | 150° |
 如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.
如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.