题目内容
9. 在一次课外实践活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离.现测得AC=300m,BC=700m,∠CAB=120°,请计算A、B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离.现测得AC=300m,BC=700m,∠CAB=120°,请计算A、B两个凉亭之间的距离.
分析 作CD⊥AB交BA的延长线于点D.根据邻补角的定义,求出∠ACD的度数,在Rt△ACD中,利用∠CAD的正弦、余弦求AD、CD,在Rt△BCD中利用勾股定理求出BD.根据线段的和差关系求出AB.
解答 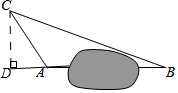 解:过点C作CD⊥BA,交BA的延长线于点D.
解:过点C作CD⊥BA,交BA的延长线于点D.
∵∠CAB=120°,∴∠CAD=60°.
在Rt△ACD中,∵sin60°=$\frac{CD}{AC}$,cos60°=$\frac{AD}{AC}$,
∴CD=sin60°×AC=$\frac{\sqrt{3}}{2}$×300=150$\sqrt{3}$(m),
AD=cos60°×AC=$\frac{1}{2}$×300=150(m)
在Rt△BCD中,BD=$\sqrt{B{C}^{2}-C{D}^{2}}$
=$\sqrt{70{0}^{2}-(150\sqrt{3)^{2}}}$=650(m)
∴AB=BD-AD=650-150=500(m)
答:A、B两个凉亭之间的距离为500m.
点评 本题考查了三角函数及勾股定理.解决本题的关键是过点C作CD⊥AB构造直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.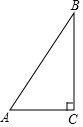 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )| A. | $\frac{36}{5}$ | B. | $\frac{12}{25}$ | C. | $\frac{9}{4}$ | D. | $\frac{3\sqrt{3}}{4}$ |
1. 如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )
如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )
 如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )
如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )| A. | 75° | B. | 90° | C. | 120° | D. | 150° |
 如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.
如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.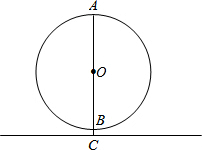 如图,⊙O是梦幻谷的摩天轮示意图,⊙O的最高处A到地面的距离是23米,最低处B到地面的距离是3米,AB是直径,摩天轮匀速转动,从B处乘坐绕摩天轮一周要6分钟,
如图,⊙O是梦幻谷的摩天轮示意图,⊙O的最高处A到地面的距离是23米,最低处B到地面的距离是3米,AB是直径,摩天轮匀速转动,从B处乘坐绕摩天轮一周要6分钟,