题目内容
某服装专卖店计划购进甲、乙两种新款服装共100件,其进价与售价如表所示:
(1)若该专卖店计划用42000元进货,则这两种新款服装各购进多少件?
(2)若乙的数量不能超过甲的数量的2倍,试问:应怎样进货才能使专卖店在销售完这批服装时获利最多?并求出最大利润.
(1)若该专卖店计划用42000元进货,则这两种新款服装各购进多少件?
(2)若乙的数量不能超过甲的数量的2倍,试问:应怎样进货才能使专卖店在销售完这批服装时获利最多?并求出最大利润.
| 价格 类型 |
进价(元/件) | 售价(元/件) |
| 甲 | 300 | 380 |
| 乙 | 500 | 600 |
考点:一次函数的应用,一元一次方程的应用,一元一次不等式的应用
专题:
分析:(1)设甲种新款服装购进x件,那么乙种新款服装购进(100-x)件,然后根据购货款列出方程求解即可;
(2)设专卖店销售完这批服装可获利w元,甲种服装m件,列式整理得到w与m的函数关系式,再求出m的取值范围,然后根据一次函数的增减性求出w的最大值即可.
(2)设专卖店销售完这批服装可获利w元,甲种服装m件,列式整理得到w与m的函数关系式,再求出m的取值范围,然后根据一次函数的增减性求出w的最大值即可.
解答:解:(1)设甲种新款服装购进x件,那么乙种新款服装购进(100-x)件,
由题意得,300x+500(100-x)=42000,
解得x=40,
当x=40时,100-x=60,
答:设甲种新款服装购进40件,乙种新款服装购进60件;
(2)设专卖店销售完这批服装可获利w元,甲种服装m件,
由题意得,w=(380-300)m+(600-500)(100-m),
整理得,w=-20m+10000,
所以,w是m的一次函数,且-20<0,
∴w随m的增大而减小,
∵乙的数量不能超过甲的数量的2倍,
∴100-m≤2m,
解得m≥33
,
∴m的取值范围是33
≤m<100,
∵m为整数,
∴m=34时,w取最大值,W最大=-20×34+10000=9320元.
答:该专卖店购进甲种服装34件,乙种服装66件,销售完这批服装获利最多,此时利润为9320元.
由题意得,300x+500(100-x)=42000,
解得x=40,
当x=40时,100-x=60,
答:设甲种新款服装购进40件,乙种新款服装购进60件;
(2)设专卖店销售完这批服装可获利w元,甲种服装m件,
由题意得,w=(380-300)m+(600-500)(100-m),
整理得,w=-20m+10000,
所以,w是m的一次函数,且-20<0,
∴w随m的增大而减小,
∵乙的数量不能超过甲的数量的2倍,
∴100-m≤2m,
解得m≥33
| 1 |
| 3 |
∴m的取值范围是33
| 1 |
| 3 |
∵m为整数,
∴m=34时,w取最大值,W最大=-20×34+10000=9320元.
答:该专卖店购进甲种服装34件,乙种服装66件,销售完这批服装获利最多,此时利润为9320元.
点评:本题考查了一次函数的应用,一元一次方程的应用,读懂题目信息,理解数量关系并确定出等量关系是解题的关键,(2)利用一次函数的增减性和自变量的取值范围求最值是常用的方法.

练习册系列答案
相关题目

 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.  小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.
小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.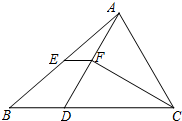 如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点.
如图,△ABC中,BC>AC,点D在BC上,且CA=CD,∠ACB的平分线交AD于点F,E是AB的中点. 如图,已知函数y=
如图,已知函数y=