题目内容

（1）解不等式组
6x+15＞2(4x+3)①
2x-1
3
≥
1
2
x-
2
3 
 ②
；         
（2）分解因式：m2（m-1）-4（1-m）2．
考点：解一元一次不等式组,整式的混合运算
专题：计算题
分析：（1）分别接两个不等式得到x＜
9
2
和x≥-2，然后根据大于小的小于大的取中间确定不等式组的解集；
（2）先提公因式（m-1），然后再利用完全平方公式分解即可．
解答：解：（1）解①得x＜
9
2
，
解②得x≥-2，
所以不等式组的解集为-2≤x＜
9
2
；
（2）原式=m2（m-1）-4（m-1）2
=（m-1）（m2-4m+4）
=（m-1）（m-2）2．
点评：本题考查了解一元一次不等式组：分别求出不等式组各不等式的解集，然后根据“同大取大，同小取小，大于小的小于大的取中间，大于大的小于小的无解”确定不等式组的解集．也考查了因式分解．
练习册系列答案
相关题目
解不等式：2（x-1）+x＞4，并把它的解集在数轴上表示出来．
为了保护环境，某开发区综合治理指挥部决定购买A、B两种型号（每种至少购买1台）的污水处理设备共10台，经调查：购买一台A型设备比购买一台B型设备多4万元，购买3台B型设备比购买2台A型设备多6万元，每台设备处理污水量如下表所示
（1）求A、B两种型号设备的价格各为多少万元？
（2）由于受资金限制，指挥部用于购买污水处理设备的资金不超过148万元，问有几种购买方案？哪种方案每月能处理的污水量最多？污水量最多为多少吨？
A型B型
处理污水量（吨/月）220180
如图1，已知∠AOC=2∠BOC，∠AOC的余角比∠BOC小30°，
（1）求∠COB的度数；
（2）经过点O作射线OD，使得∠AOC=4∠AOD，求∠BOD的度数；
（3）如图2，在∠AOB的内部作∠EOF，OM、ON分别为∠AOE和∠BOF的平分线，当∠EOF绕点O在∠AOB的内部转动时，请说明∠AOB+∠EOF=2∠MON．
不透明的口袋里装有红、黄、蓝三种颜色的小球共4个（除颜色外其他都相同），其中红球2个（分别标有1号、2号），黄球、蓝求各1个．
（1）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表的方法，求两次摸到不同颜色球的概率；
（2）第一次任意摸一个球，然后放回去，混合后第二次再摸出一个球，求两次摸到的球为一个黄球和一个蓝球的概率（不写解题过程，直接写出结论）．
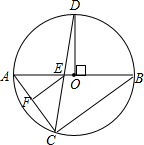在⊙O中，已知AB为直径，C、D是⊙O上两点，且C、D在AB的两侧，OD⊥AB，CD交AB于E点，过E作EF∥BC交AC于F点．
（1）求证：CD平分∠ACB；
（2）若AF：CF=1：2，且CE=2，求△ACE的面积．
（1）计算：-32+（
1
2
）-1-|-3|-（1-x）0；
（2）计算：（-
3
2
ab2）2÷（3b2）2•（-8ab）．
如果一个四边形的两条对角线长分别为7cm和12cm，那么顺次联结这个四边形各边中点所得四边形的周长是
 
cm．
如图，正方形ABCD的面积为S，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网