题目内容
如图1,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°,
(1)求∠COB的度数;
(2)经过点O作射线OD,使得∠AOC=4∠AOD,求∠BOD的度数;
(3)如图2,在∠AOB的内部作∠EOF,OM、ON分别为∠AOE和∠BOF的平分线,当∠EOF绕点O在∠AOB的内部转动时,请说明∠AOB+∠EOF=2∠MON.
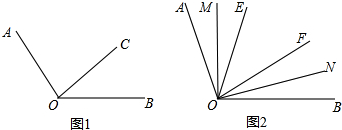
(1)求∠COB的度数;
(2)经过点O作射线OD,使得∠AOC=4∠AOD,求∠BOD的度数;
(3)如图2,在∠AOB的内部作∠EOF,OM、ON分别为∠AOE和∠BOF的平分线,当∠EOF绕点O在∠AOB的内部转动时,请说明∠AOB+∠EOF=2∠MON.

考点:角的计算,角平分线的定义
专题:
分析:(1)设∠BOC=x,则∠AOC=2x,根据,∠AOC的余角比∠BOC小30゜列方程求解即可;
(2)分两种情况:①当射线OD在∠AOC内部②当射线OD在∠AOC外部,分别求出∠BOD的度数即可;
(3)OM、ON分别为∠AOE和∠BOF的平分线,可得∠MOE=
∠AOE,∠FON=
∠BOF,所以∠MON=∠EOF+
(∠AOE+∠BOF),即可得2∠MON=2∠EOF+∠AOE+∠BOF=∠AOB+∠EOF.
(2)分两种情况:①当射线OD在∠AOC内部②当射线OD在∠AOC外部,分别求出∠BOD的度数即可;
(3)OM、ON分别为∠AOE和∠BOF的平分线,可得∠MOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)设∠BOC=x,则∠AOC=2x,
依题意列方程90°-2x=x-30°,
解得:x=40°,
即∠COB=40゜.
(2)由(1)得,∠AOC=80°,∠AOB=∠AOC+∠BOC=120°,
①当射线OD在∠AOC内部时,∠AOD=20゜,
则∠BOD=∠AOB-∠AOD=120°-20°=100°;
②当射线OD在∠AOC外部时,∠AOD=20゜
则∠BOD=∠AOB+∠AOD=120゜+20°=140°;
(3)∵OM、ON分别为∠AOE和∠BOF的平分线,
∴∠MOE=
∠AOE,∠FON=
∠BOF,
∴∠MON=∠EOF+
(∠AOE+∠BOF),
∴2∠MON=2∠EOF+∠AOE+∠BOF=∠AOB+∠EOF.
即∠AOB+∠EOF=2∠MON.
依题意列方程90°-2x=x-30°,
解得:x=40°,
即∠COB=40゜.
(2)由(1)得,∠AOC=80°,∠AOB=∠AOC+∠BOC=120°,
①当射线OD在∠AOC内部时,∠AOD=20゜,
则∠BOD=∠AOB-∠AOD=120°-20°=100°;
②当射线OD在∠AOC外部时,∠AOD=20゜
则∠BOD=∠AOB+∠AOD=120゜+20°=140°;
(3)∵OM、ON分别为∠AOE和∠BOF的平分线,
∴∠MOE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠EOF+
| 1 |
| 2 |
∴2∠MON=2∠EOF+∠AOE+∠BOF=∠AOB+∠EOF.
即∠AOB+∠EOF=2∠MON.
点评:本题考查了角平分线的定义以及角的计算,还用到了方程的思想.注意(2)要根据射线OD的位置不同,分类讨论,分别求出∠BOD的度数.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
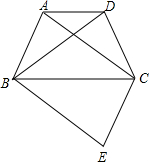 如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业). 阅读理解
阅读理解