题目内容
为了保护环境,某开发区综合治理指挥部决定购买A、B两种型号(每种至少购买1台)的污水处理设备共10台,经调查:购买一台A型设备比购买一台B型设备多4万元,购买3台B型设备比购买2台A型设备多6万元,每台设备处理污水量如下表所示
(1)求A、B两种型号设备的价格各为多少万元?
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过148万元,问有几种购买方案?哪种方案每月能处理的污水量最多?污水量最多为多少吨?
(1)求A、B两种型号设备的价格各为多少万元?
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过148万元,问有几种购买方案?哪种方案每月能处理的污水量最多?污水量最多为多少吨?
| A型 | B型 | |
| 处理污水量(吨/月) | 220 | 180 |
考点:一元一次不等式的应用,二元一次方程组的应用
专题:
分析:(1)设A、B两种型号设备的价格各为x万元,y万元,根据购买一台A型设备比购买一台B型设备多4万元,购买3台B型设备比购买2台A型设备多6万元,列方程组求解;
(2)设购买A型号a台,B型号(10-a)台,根据总资金不超过148万元,列不等式,求出a的取值范围,然后求出购买方案.
(2)设购买A型号a台,B型号(10-a)台,根据总资金不超过148万元,列不等式,求出a的取值范围,然后求出购买方案.
解答:解:(1)设A、B两种型号设备的价格各为多x万元,y万元,
由题意得,
,
解得:
,
答:A、B两种型号设备的价格各为18万元,14万元;
(2)设购买A型号a台,B型号(10-a)台,
由题意得,18a+14(10-a)≤148,
解得:a≤2,
则共有2种购买方案:A种型号买1台,B种型号买9台,处理污水量为:220+180×9=1840(吨);
A种型号买2台,B种型号买8台,处理污水量为:220×2+180×8=1880(吨).
答:A种型号买2台,B种型号买8台,处理污水量最多,为1880吨.
由题意得,
|
解得:
|
答:A、B两种型号设备的价格各为18万元,14万元;
(2)设购买A型号a台,B型号(10-a)台,
由题意得,18a+14(10-a)≤148,
解得:a≤2,
则共有2种购买方案:A种型号买1台,B种型号买9台,处理污水量为:220+180×9=1840(吨);
A种型号买2台,B种型号买8台,处理污水量为:220×2+180×8=1880(吨).
答:A种型号买2台,B种型号买8台,处理污水量最多,为1880吨.
点评:本题考查了一元一次不等式和二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出题目中的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
在π、-2.5、-
、
这四个数中,属于负分数的是( )
| 2 |
| 3 |
| 4 |
| A、π | ||
| B、-2.5 | ||
C、-
| ||
D、
|
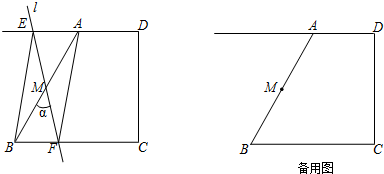
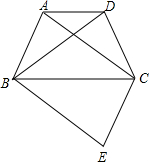 如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如图尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).