题目内容
不透明的口袋里装有红、黄、蓝三种颜色的小球共4个（除颜色外其他都相同），其中红球2个（分别标有1号、2号），黄球、蓝求各1个．
（1）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表的方法，求两次摸到不同颜色球的概率；
（2）第一次任意摸一个球，然后放回去，混合后第二次再摸出一个球，求两次摸到的球为一个黄球和一个蓝球的概率（不写解题过程，直接写出结论）．
（1）第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表的方法，求两次摸到不同颜色球的概率；
（2）第一次任意摸一个球，然后放回去，混合后第二次再摸出一个球，求两次摸到的球为一个黄球和一个蓝球的概率（不写解题过程，直接写出结论）．
考点：列表法与树状图法
专题：
分析：（1）用列表法或画出树状图，然后根据概率公式列式计算即可得解；
（2）根据（1）中的图表即可求出求两次摸到的球为一个黄球和一个蓝球的概率．
（2）根据（1）中的图表即可求出求两次摸到的球为一个黄球和一个蓝球的概率．
解答：解：（1）列表如下：
所以两次摸到不同颜色球的概率为：P=
=
．
（2）两次摸到一个黄球和一个蓝球的概率P=
=
．
| 第2次 第1次 | 红1 | 红2 | 黄 | 蓝 |
| 红1 | （红1，红2） | （红1，黄） | （红1，蓝） | |
| 红2 | （红2，红1） | （红2，黄） | （红2，蓝） | |
| 黄 | （黄，红1） | （黄，红2） | （黄，蓝） | |
| 蓝 | （蓝，红1） | （蓝，红2） | （蓝，黄） |
| 10 |
| 12 |
| 5 |
| 6 |
（2）两次摸到一个黄球和一个蓝球的概率P=
| 2 |
| 16 |
| 1 |
| 8 |
点评：此题考查了列表法与树状图法，以及概率公式，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
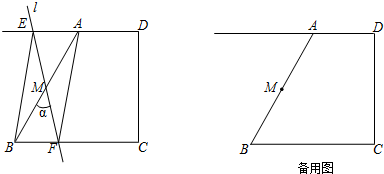
某社区准备在甲、乙两位射箭爱好者中选出一人参加集训，两人各射了5箭，他们的总成绩（单位：环）相同，小宇根据他们的成绩绘制了如图尚不完整的统计图表，并计算了甲成绩的平均数和方差（见小宇的作业）．
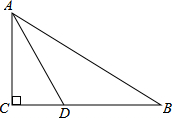如图，在Rt△ABC中，∠B=90°，AD平分∠BAC，∠BAD=α，sinα=