题目内容
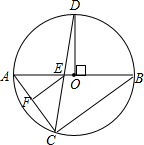 在⊙O中,已知AB为直径,C、D是⊙O上两点,且C、D在AB的两侧,OD⊥AB,CD交AB于E点,过E作EF∥BC交AC于F点.
在⊙O中,已知AB为直径,C、D是⊙O上两点,且C、D在AB的两侧,OD⊥AB,CD交AB于E点,过E作EF∥BC交AC于F点.(1)求证:CD平分∠ACB;
(2)若AF:CF=1:2,且CE=2,求△ACE的面积.
考点:圆的综合题
专题:
分析:(1)利用垂径定理得出
=
,进而得出∠ACD=∠BCD得出答案即可;
(2)首先得出EF=FC,利用勾股定理求出其长度,进而得出AC的长,最后求出三角形面积.
 |
| AD |
 |
| BD |
(2)首先得出EF=FC,利用勾股定理求出其长度,进而得出AC的长,最后求出三角形面积.
解答:(1)证明:∵AB为直径,OD⊥AB,
∴OD平分弧AB,即
=
,
∴∠ACD=∠BCD(弧相等,对应的角也相等)
即CD平分∠ACB;
(2)解:∵AB为直径,
∴∠ACB=90°,
∴∠ACD=∠BCD=45°,
∵EF∥BC,
∴∠EFC=90°,
∴∠FEC=45°,
∴EF=FC,
∴EC=2,
∴EF=FC=
,
∵AF:CF=1:2,
∴AF=
,
∴AC=AF+FC=
,
∴S△AEC=
×EF×AC=
×
×
=
.
∴OD平分弧AB,即
 |
| AD |
 |
| BD |
∴∠ACD=∠BCD(弧相等,对应的角也相等)
即CD平分∠ACB;
(2)解:∵AB为直径,
∴∠ACB=90°,

∴∠ACD=∠BCD=45°,
∵EF∥BC,
∴∠EFC=90°,
∴∠FEC=45°,
∴EF=FC,
∴EC=2,
∴EF=FC=
| 2 |
∵AF:CF=1:2,
∴AF=
| ||
| 2 |
∴AC=AF+FC=
3
| ||
| 2 |
∴S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
点评:此题主要考查了圆的综合应用以及勾股定理和垂径定理等知识,得出EF=FC的长是解题关键.

练习册系列答案
相关题目
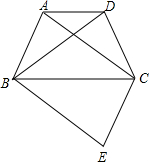 如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC. 阅读理解
阅读理解