题目内容
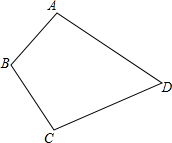 有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?考点:作图—应用与设计作图,三角形三边关系
专题:
分析:连接AC、BD相交于点P,则点P就是所要找的点;
取不同于点P的任意一点O,连接OA、OB、OC、OD,根据三角形任意两边之和大于第三边可得OA+OC>AC,OB+OD>BD,然后结合图形即可得到OA+OB+OC+OD>PA+PB+PC+PD,从而可得点P就是所要找的四边形ABCD内符合要求的点.
取不同于点P的任意一点O,连接OA、OB、OC、OD,根据三角形任意两边之和大于第三边可得OA+OC>AC,OB+OD>BD,然后结合图形即可得到OA+OB+OC+OD>PA+PB+PC+PD,从而可得点P就是所要找的四边形ABCD内符合要求的点.
解答: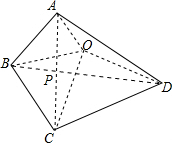 解:要使PA+PB+PC+PD最小,则点P是线段AC、BD的交点.
解:要使PA+PB+PC+PD最小,则点P是线段AC、BD的交点.
理由如下:如果存在不同于点P的交点O,连接OA、OB、OC、OD,
那么OA+OC>AC,
即OA+OC>PA+PC,
同理,OB+OD>PB+PD,
∴OA+OB+OC+OD>PA+PB+PC+PD,
即点P是线段AC、BD的交点时,PA+PB+PC+PD之和最小.
 解:要使PA+PB+PC+PD最小,则点P是线段AC、BD的交点.
解:要使PA+PB+PC+PD最小,则点P是线段AC、BD的交点.理由如下:如果存在不同于点P的交点O,连接OA、OB、OC、OD,
那么OA+OC>AC,
即OA+OC>PA+PC,
同理,OB+OD>PB+PD,
∴OA+OB+OC+OD>PA+PB+PC+PD,
即点P是线段AC、BD的交点时,PA+PB+PC+PD之和最小.
点评:本题考查了三角形的任意两边之和大于第三边的性质,作出图形更助于问题的解决,本题渗透了反证法的思想,希望同学们逐渐适应并熟练掌握.

练习册系列答案
相关题目
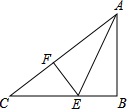 如图,AE为∠BAC的平分线,EB⊥AB,EF⊥AC,则下列结论不正确的是( )
如图,AE为∠BAC的平分线,EB⊥AB,EF⊥AC,则下列结论不正确的是( )| A、EF=EB |
| B、AF=AB |
| C、AE=CE |
| D、∠AEF=∠AEB |
 如图,在⊙O中,直径AB⊥弦CD于点E.若BE=
如图,在⊙O中,直径AB⊥弦CD于点E.若BE=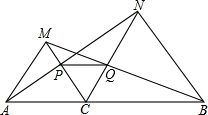 如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.
如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.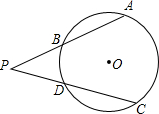 如图,P为⊙O外一点,∠APC的两边分别交⊙O于点A,B和C,D.如果PA=PC,求证:AB=CD.
如图,P为⊙O外一点,∠APC的两边分别交⊙O于点A,B和C,D.如果PA=PC,求证:AB=CD.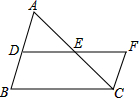 在△ABC中,点D,E分别是AB,AC的中点,连接DE并延长到点F,使EF=DE,连接CF.
在△ABC中,点D,E分别是AB,AC的中点,连接DE并延长到点F,使EF=DE,连接CF.