题目内容
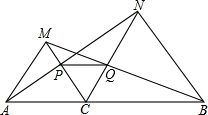 如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.
如图,点C在线段AB上,以AC和BC为边在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM,分别交CM,CN于点P,Q.△ACN和△MCB全等吗?说明理由.考点:全等三角形的判定,等边三角形的性质
专题:
分析:根据等边三角形的性质得到∠ACM=∠BCN=60°,CA=CM,CN=CB,可得到∠MCN=60°,则∠ACN=∠BCM=120°,然后根据“SAS”可证明△ACN≌△MCB.
解答: 解:△ACN和△MCB全等;
解:△ACN和△MCB全等;
理由:∵△ACM和△BCN都是等边三角形,
∴∠ACM=∠BCN=60°,CA=CM,CN=CB,
∴∠MCN=60°,
∴∠ACN=∠BCM=120°,
∵在△ACN和△MCB中,
,
∴△ACN≌△MCB(SAS).
 解:△ACN和△MCB全等;
解:△ACN和△MCB全等;理由:∵△ACM和△BCN都是等边三角形,
∴∠ACM=∠BCN=60°,CA=CM,CN=CB,
∴∠MCN=60°,
∴∠ACN=∠BCM=120°,
∵在△ACN和△MCB中,
|
∴△ACN≌△MCB(SAS).
点评:本题考查了等边三角形的性质以及全等三角形的判定与性质:有两组边对应相等,且它们所夹的角也相等,那么这两个三角形全等.

练习册系列答案
相关题目
下列说法正确的是( )
| A、旋转后重合的两个图形成中心对称 |
| B、全等的两个图形一定成中心对称 |
| C、成中心对称的两个图形一定全等 |
| D、正三角形是中心对称图形 |
 如图,AD∥BC,∠D=90°,DC=5,AD=2,BC=3,点P在线段DC上,问:当PC的长为何值时,△PAD与△PBC相似?
如图,AD∥BC,∠D=90°,DC=5,AD=2,BC=3,点P在线段DC上,问:当PC的长为何值时,△PAD与△PBC相似?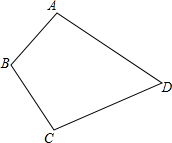 有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?