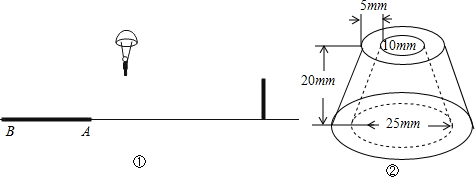
题目内容
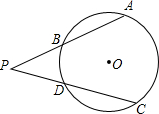 如图,P为⊙O外一点,∠APC的两边分别交⊙O于点A,B和C,D.如果PA=PC,求证:AB=CD.
如图,P为⊙O外一点,∠APC的两边分别交⊙O于点A,B和C,D.如果PA=PC,求证:AB=CD.考点:全等三角形的判定与性质,角平分线的性质,垂径定理
专题:证明题
分析:连结OP,AC,作OE⊥AB于E,OF⊥CD于F.根据等腰三角形的性质及△POE≌△POF全等三角形的性质就可以得出结论.
解答:解:连结OP,AC,作OE⊥AB于E,OF⊥CD于F.
∴∠OEP=∠OFP=90°.
∵PA=PC,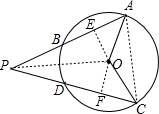
∴∠PAC=∠PCA.
∵∠OAC=∠OCA,
∴∠PAC-∠OAC=∠PCA-∠OCA,
∴∠PAO=∠PCO.
在△POA和△POC中,
,
∴△POA≌△POC(SAS)
∴∠APO=∠CPO.
在△POE和△POF中
,
∴△POB≌△POD(AAS),
∴OE=OF.
∵OE⊥AB,OF⊥CD,
∴AB=CD.
∴∠OEP=∠OFP=90°.
∵PA=PC,

∴∠PAC=∠PCA.
∵∠OAC=∠OCA,
∴∠PAC-∠OAC=∠PCA-∠OCA,
∴∠PAO=∠PCO.
在△POA和△POC中,
|
∴△POA≌△POC(SAS)
∴∠APO=∠CPO.
在△POE和△POF中
|
∴△POB≌△POD(AAS),
∴OE=OF.
∵OE⊥AB,OF⊥CD,
∴AB=CD.
点评:本题考查了等腰三角形的性质的运用,角平分线的判定及性质的运用,垂径定理的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
已知(x-y+3)2+
=0,则x+y的值为( )
| 2x+y |
| A、0 | B、-1 | C、1 | D、2 |
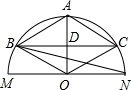 如图,MN为半圆O的直径,半径0A⊥MN,D为OA的中点,过点D作BC∥MN.求证:
如图,MN为半圆O的直径,半径0A⊥MN,D为OA的中点,过点D作BC∥MN.求证: 有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗?
有四个汽车停车场,位于如图所示的四边形ABCD的四个顶点,现在要建立一个汽车维修站,你能利用“三角形任意两边之和大于第三边”,在四边形ABCD的内部找一点P,使点P到A,B,C,D四点的距离之和最小吗? 如图,把图中的四边形ABCD以点O为位似中心,沿AO方向放大到原来的2倍(即位似比为2).
如图,把图中的四边形ABCD以点O为位似中心,沿AO方向放大到原来的2倍(即位似比为2). 如图,在直线MN上找一点P,使点P到直线AB和直线CD的距离相等.
如图,在直线MN上找一点P,使点P到直线AB和直线CD的距离相等.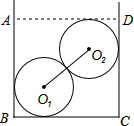 某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个
某人用如下方法测一钢管的内径:将一小段钢管竖直放在平台上,向内放入两个