题目内容
9.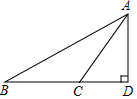 如图,在△ABD中,∠D=90°,CD=6,AD=8,∠ACD=2∠B,则BD的长是( )
如图,在△ABD中,∠D=90°,CD=6,AD=8,∠ACD=2∠B,则BD的长是( )| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
分析 根据勾股定理求出AC,根据三角形的外角的性质得到∠B=∠CAB,根据等腰三角形的性质求出BC,计算即可.
解答 解:∵∠D=90°,CD=6,AD=8,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=10,
∵∠ACD=2∠B,∠ACD=∠B+∠CAB,
∴∠B=∠CAB,
∴BC=AC=10,
∴BD=BC+CD=16,
故选:C.
点评 本题考查的是勾股定理、三角形的外角的性质,直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
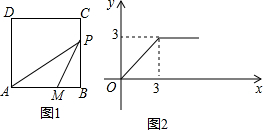 如图1,四边形ABCD是正方形,M是边AB上一点,AM=2cm,动点P从点B出发,以每秒acm的速度沿BC-CD-DA运动到点A停止,△AMP的面积y(cm2)与动点P的运动时间x(秒)的关系如图2(部分)所示.
如图1,四边形ABCD是正方形,M是边AB上一点,AM=2cm,动点P从点B出发,以每秒acm的速度沿BC-CD-DA运动到点A停止,△AMP的面积y(cm2)与动点P的运动时间x(秒)的关系如图2(部分)所示. 已知:如图,直线y=-$\frac{1}{2}$x-3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0).
已知:如图,直线y=-$\frac{1}{2}$x-3与坐标轴交于点A,C,经过点A,C的抛物线y=ax2+bx-3与x轴交于点B(2,0). 如图,在平面直角坐标系中,边长为4的正方形AOCB的顶点A、C分别在y轴和x轴上,E为边AB上的一点且AE=3,反比例函数y=$\frac{m}{x}$(x>0)的图象过点E.
如图,在平面直角坐标系中,边长为4的正方形AOCB的顶点A、C分别在y轴和x轴上,E为边AB上的一点且AE=3,反比例函数y=$\frac{m}{x}$(x>0)的图象过点E.