题目内容
18. 如图,在平面直角坐标系中,边长为4的正方形AOCB的顶点A、C分别在y轴和x轴上,E为边AB上的一点且AE=3,反比例函数y=$\frac{m}{x}$(x>0)的图象过点E.
如图,在平面直角坐标系中,边长为4的正方形AOCB的顶点A、C分别在y轴和x轴上,E为边AB上的一点且AE=3,反比例函数y=$\frac{m}{x}$(x>0)的图象过点E.(1)求反比例函数的解析式;
(2)反比例函数y=$\frac{m}{x}$(x>0)的图象与线段BC交于点D,且与过点D的直线y=kx+b相切,直线y=kx+b与线段AB相交于点F,求点F的坐标;
(3)连接OF、OE,试问在直线y=kx+b是否存在一点G,使S△OCG=3S△OFE,若存在,求出点G的坐标;若不存在,请说明理由.
分析 (1)求出点E坐标,利用待定系数法即可解决问题;
(2)由题意可知一次函数为y=kx+3-4k,由$\left\{\begin{array}{l}{y=\frac{12}{x}}\\{y=kx+3-4k}\end{array}\right.$,消去y得到kx2+(3-4k)x-12=0,根据△=0求出k即可解决问题;
(3)设G(m,-$\frac{3}{4}$m+6),由题意$\frac{1}{2}$×4×|-$\frac{3}{4}$m+6|=3×$\frac{1}{2}$×$\frac{1}{3}$×4,解方程求出m即可解决问题;
解答 解:(1)由题意E(3,4),
∵反比例函数y=$\frac{m}{x}$(x>0)的图象过点E,
∴4=$\frac{m}{3}$,
∴m=12,
∴反比例函数的解析式为y=$\frac{12}{x}$.
(2)∵反比例函数的解析式为y=$\frac{12}{x}$的图象与线段BC交于点D
∴D(4,3),
∵直线y=kx+b经过D(4,3),
∴4k+b=3,
∴b=3-4k,
∴一次函数为y=kx+3-4k,
由$\left\{\begin{array}{l}{y=\frac{12}{x}}\\{y=kx+3-4k}\end{array}\right.$,消去y得到kx2+(3-4k)x-12=0,
由题意△=0,
∴(3-4k)2+48k=0,
解得k=-$\frac{3}{4}$,
∴一次函数的解析式为y=-$\frac{3}{4}$x+6,
∴F($\frac{8}{3}$,4).
(3)设G(m,-$\frac{3}{4}$m+6),
由题意$\frac{1}{2}$×4×|-$\frac{3}{4}$m+6|=3×$\frac{1}{2}$×$\frac{1}{3}$×4,解得m=$\frac{20}{3}$或$\frac{28}{3}$,
∴G($\frac{20}{3}$,1)或($\frac{28}{3}$,-1).
点评 本题考查反比例函数综合题、一次函数的应用、正方形的性质、一元二次方程的根的判别式等知识,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中考常考题型.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案| A. | 互为相反数 | B. | 相等 | C. | 互为倒数 | D. | 无法判断 |
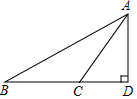 如图,在△ABD中,∠D=90°,CD=6,AD=8,∠ACD=2∠B,则BD的长是( )
如图,在△ABD中,∠D=90°,CD=6,AD=8,∠ACD=2∠B,则BD的长是( )| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
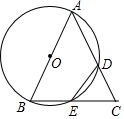 如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.
如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.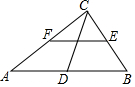 如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,AC的中点,若CD=7cm,则EF=7cm.
如图,在Rt△ABC中,∠ACB=90°,D,E,F分别是AB,BC,AC的中点,若CD=7cm,则EF=7cm.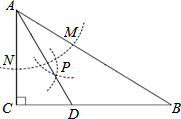 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论正确的有( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论正确的有( )