题目内容
4．若关于x，y的二元一次方程组$\left\{\begin{array}{l}{2x+y=-3k+1}\\{x+2y=2}\end{array}\right.$的解满足x+y＞2，则k的取值范围是k＜-1．分析 两方程相加得出x+y=-k+1，由x+y＞2得到关于k的不等式，解之可得．
解答 解：将方程组中两方程相加可得：3x+3y=-3k+3，
则x+y=-k+1，
∵x+y＞2，
∴-k+1＞2，
解得：k＜-1，
故答案为：k＜-1．
点评 本题主要考查解一元一次不等式的能力，根据题意得出关于k的方程是解题的关键．
练习册系列答案
相关题目
14．给出一列数0，$\frac{3}{2}$，$\frac{8}{3}$，$\frac{15}{4}$，$\frac{24}{5}$，…，第六个数为（ ）
| A． | $\frac{33}{6}$ | B． | $\frac{35}{6}$ | C． | 12 | D． | $\frac{37}{6}$ |
利用数轴解不等式|x-1|＞2．
12．某地某一时刻的地面温度为10℃，高度每增加1km，温度下降4℃，则下列说法中：①10℃是常量；②高度是变量；③温度是变量；④该地某一高度这一时刻的温度y（℃）与高度x（km）的关系式为y=10-4x；正确的是（ ）
| A． | ①②③ | B． | ②③④ | C． | ①③④ | D． | ①②③④ |
9．
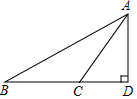如图，在△ABD中，∠D=90°，CD=6，AD=8，∠ACD=2∠B，则BD的长是（ ）
如图，在△ABD中，∠D=90°，CD=6，AD=8，∠ACD=2∠B，则BD的长是（ ）| A． | 12 | B． | 14 | C． | 16 | D． | 18 |
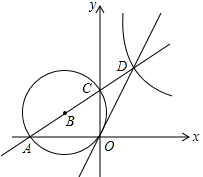已知：如图，O为平面直角坐标系的原点，半径为1的⊙B经过点O，且与x，y轴分别交于点A，C，点A的坐标为（-$\sqrt{3}$，0），AC的延长线与⊙B的切线OD交于点D．