题目内容
8.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边作正方形ADEF,连接CF.(1)如图1,当点D在线段BC上时.求证:CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,则CF,BC,CD三条线段之间有什么关系?并说明理由.

分析 (1)如图1,由∠BAC=90°,∠ABC=45°可得AB=AC,再根据正方形性质得AD=AF,∠DAF=90°,接着根据等角的余角相等得∠BAD=∠CAF,于是可根据“SAS”判断△BAD≌△CAF,得到BD=CF,所以CF+CD=BD+CD=BC;
(2)和(1)的方法一样可证明△BAD≌△CAF得到BD=CF,而BD=BC+CD,则CF-CD=BC.
解答 (1)证明:如图1,
∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°-∠DAC,∠CAF=90°-∠DAC,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∵BD+CD=BC,
∴CF+CD=BC;
(2)解:CF-CD=BC.理由如下:
如图2,
∵∠BAD=90°+∠CAD,
∠CAF=90°+∠CAD,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∵BD=BC+CD,
∴CF-CD=BC.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

 名校课堂系列答案
名校课堂系列答案(1)给定x的一些值,请计算y的值,填在表中
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | 160 | 140 | 120 | 100 | 80 | … |
(3)当商品的销售单价定为多少元时,该商品销售这种商品能获得的利润为420元?这时每天销售的商品是多少件?
| A. | x1=x2=1 | B. | x1=x2=-2 | C. | x1=x2=-1 | D. | x1=x2=2 |
| A. | 4 | B. | $\frac{24}{5}$ | C. | $\frac{40}{3}$ | D. | $\frac{15}{2}$ |
 四边形ABCO中,BC∥AO,BC与OA间的距离为$\sqrt{3}$,OA=6,∠AOC=60°,∠OAB=30°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒).
四边形ABCO中,BC∥AO,BC与OA间的距离为$\sqrt{3}$,OA=6,∠AOC=60°,∠OAB=30°,动点P从点O以每秒2个单位的速度向点A运动,动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动,当点P到达A点时,点Q也随之停止,设点P,Q运动的时间为t(秒). 小明从家骑自行车出发,沿一条直路到相距2400米的移动公司办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局同一条道路步行回家,小明在邮局停留2分钟后沿原路原原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD,线段EF分别表示S1、S2与t之间的函数关系的图象.
小明从家骑自行车出发,沿一条直路到相距2400米的移动公司办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局同一条道路步行回家,小明在邮局停留2分钟后沿原路原原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD,线段EF分别表示S1、S2与t之间的函数关系的图象.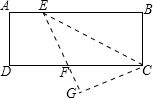 如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.
如图,在长方形ABCD中,E为AB上一点,把三角形CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,则∠BCE的度数为50°.