题目内容
5. 如图,抛物线y=2x2-m的顶点为P,与x轴交于点A,B,且△ABP是等腰直角三角形,则m的值是( )
如图,抛物线y=2x2-m的顶点为P,与x轴交于点A,B,且△ABP是等腰直角三角形,则m的值是( )| A. | -2 | B. | $\frac{1}{2}$ | C. | 2 | D. | -$\frac{1}{2}$ |
分析 观察抛物线的解析式,它的开口向上,由于与x轴交于点A,B,得m>0,△ABP是等腰直角三角形,必须满足顶点纵坐标的绝对值与点B横坐标相等,以此作为等量关系来列方程解出m的值.
解答 解:∵抛物线解析式为y=2x2-m,
∴该抛物线的顶点P的坐标为(0,-m),
∵抛物线和x轴有两个交点,
∴△=0-4×2(-m)>0,
∴m>0,
令y=0,得x=±$\frac{\sqrt{2m}}{2}$,
又∵△ABP是等腰直角三角形,
∴$\frac{\sqrt{2m}}{2}$=m,
解得 m=$\frac{1}{2}$,
故选B.
点评 本题考查了抛物线与x轴的交点.此题利用“等腰直角三角形斜边上的中线等于斜边的一半”列出的等式.

练习册系列答案
相关题目
15.下列关于函数y=$\frac{1}{2}$(x-6)2+3的图象,下列叙述错误的是( )
| A. | 图象是抛物线,开口向上 | |
| B. | 对称轴为直线x=6 | |
| C. | 顶点是图象的最高点,坐标为(6,3) | |
| D. | 当x<6时,y随x的增大而减小;当x>6时,y随x的增大而增大 |
10.用配方法解方程x2+x-1=0,配方后所得方程是( )
| A. | (x-$\frac{1}{2}$)2=$\frac{3}{4}$ | B. | (x+$\frac{1}{2}$)2=$\frac{3}{4}$ | C. | (x-$\frac{1}{2}$)2=$\frac{5}{4}$ | D. | (x+$\frac{1}{2}$)2=$\frac{5}{4}$ |
15.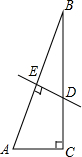 如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=8cm,则AC等于( )
如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=8cm,则AC等于( )
 如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=8cm,则AC等于( )
如图,在△ABC,∠C=90°,∠B=15°,AB的中垂线DE交BC于D,E为垂足,若BD=8cm,则AC等于( )| A. | 8cm | B. | 6cm | C. | 4cm | D. | 2.5cm |
 如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE.
如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 如图:反比例函数y=$\frac{6}{x}$的图象如下,在图象上任取一点P,过P点作x轴的垂线交x轴于M,则三角形OMP的面积为( )
如图:反比例函数y=$\frac{6}{x}$的图象如下,在图象上任取一点P,过P点作x轴的垂线交x轴于M,则三角形OMP的面积为( )
