题目内容

15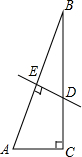．如图，在△ABC，∠C=90°，∠B=15°，AB的中垂线DE交BC于D，E为垂足，若BD=8cm，则AC等于（　　）
A．8cmB．6cmC．4cmD．2.5cm

分析 连接AD，先由三角形内角和定理求出∠BAC的度数，再由线段垂直平分线的性质可得出∠DAB的度数，根据线段垂直平分线的性质可求出AD的长及∠DAC的度数，最后由直角三角形的性质即可求出AC的长．

解答 解：连接AD，
∵DE是线段AB的垂直平分线，BD=8，∠B=15°，
∴AD=BD=10，
∴∠DAB=∠B=15°，
∴∠ADC=∠B+∠DAB=15°+15°=30°，
∵∠C=90°，
∴AC=$\frac{1}{2}$AD=4cm．
故选C．

点评 本题考查的是直角三角形的性质及线段垂直平分线的性质，熟知线段垂直平分的性质是解答此题的关键．

练习册系列答案
相关题目
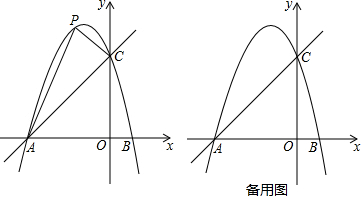
5．如图，抛物线y=2x2-m的顶点为P，与x轴交于点A，B，且△ABP是等腰直角三角形，则m的值是（　　）
A．-2B．$\frac{1}{2}$C．2D．-$\frac{1}{2}$
6．如图，一棵树在一次强台风中，从离地面3米折断，量得倒下部分树尖与树根的距离是4米，这棵树在折断前的高度是（　　）
A．7米B．8米C．9米D．10米
3．把多项式x2-6x+9分解因式，结果正确的是（　　）
A．（x+3）（x-3）B．（x-9）2C．（x-3）2D．（x+9）（x-9）
10．把方程（x-1）2-3x=（2x+1）2化成一般形式，并写出各项系数及常数项a，b，c的值．
20．如图，二次函数y=-x2+bx+c的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，OB=1，OC=3．
（1）求抛物线的解析式；
（2）如图，点P为抛物线上的一点，且在直线AC上方，当△ACP的面积是$\frac{27}{8}$时，求点的坐标；
（3）是否存在抛物线上的点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由．
7．如图1，点A（0，a），B（-a，0）分别在y轴，x轴上（a＞0），以AB为对角线作长方形ACBD，点C在第二象限内运动．
（1）若方程$\frac{x+4}{x-2}$+1=$\frac{x-14}{2-x}$的解是a，求A，B两点的坐标；
（2）延长BD交y轴于E，AD交x轴于F，连结EF，求证：EF⊥AB；
（3）如图2，连结OD，求∠ODA的度数．
6．一个密闭不透明盒子中有若干个白球，现又放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再放回盒中，像这样共摸200次，其中40次摸到黑球，估计盒中大约有白球（　　）
A．28个B．30个C．32个D．34个
7．若多项式与单项式2a2b的积是6a3b-a2b2，则该多项式为3a-$\frac{1}{2}$b．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网