题目内容
20.如图,在日历中用一个正方形任意圈出四个数得到一个2×2列表,如:| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | | |
| 8 | 9 |
| 15 | 16 |
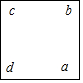
(1)分别用含a的代数式表示b,c,d这三个数:
b=a-7,c=a-8,d=a-1.
(2)求这四个数的和(用含a的代数式表示,要求合并同类项化简);
(3)这四个数的和会等于16吗?如果会,请算出此时a的值;如果不会,说明理由.(要求列方程解答)
分析 (1)日历上每一竖列较大的数减去较小的数都等于7,横行上相邻的数都相隔1,据此可得;
(2)根据(1)中结果,将四个数相加后,由整式的加减运算化简可得;
(3)根据题意列出方程,解方程后根据实际意义取舍即可判断.
解答 解:(1)b=a-7,c=a-8,d=a-1,
故答案为:a-7,a-8,a-1;
(2)这四个数的和为a+a-8+a-7+a-1=4a-16;
(3)不会,
当4a-16=16时,解得:a=0,
由题意知a≥9,
故不存在这样的a使得四个数的和等于16.
点评 本题主要考查列代数式和一元一次方程的应用,根据题意能表示出圈出的四个数及利用方程求解是解题的关键.

练习册系列答案
相关题目
 如图,将边长为4的等边三角形AOB放置于平面直角坐标系xOy中,F是AB边上的动点(不与端点A、B重合),过点F的反比例函数y=$\frac{k}{x}$(k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.
如图,将边长为4的等边三角形AOB放置于平面直角坐标系xOy中,F是AB边上的动点(不与端点A、B重合),过点F的反比例函数y=$\frac{k}{x}$(k>0,x>0)与OA边交于点E,过点F作FC⊥x轴于点C,连结EF、OF.