题目内容
12.如图,平面直角坐标系中,一次函数y=2x+6的图象与x轴交于点A,与y轴交于点B,点C是直线AB上的一点,它的坐标为(m,4),经过点C作直线CD∥x轴交y轴于点D.(1)求点C的坐标及线段AB的长;
(2)已知点P是直线CD上一点.
请从A、B两个题目中任选一题作答.
A.①若△POC的面积为4,求点P的坐标;
②若△POC上直角三角形,请直接写出所有满足条件的点P的坐标.
B.①若△PAB的面积为6,求点P的坐标;
②若△PAB是等腰三角形,请直接写出所有满足条件的点P的坐标.
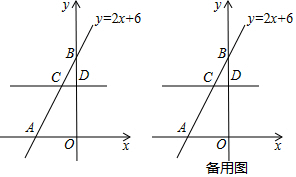
分析 (1)把(m,4)代入y=2x+6得2m+6=4,即可求出点C坐标,求出A、B两点坐标,利用两点间距离公式即可求出AB的长.
(2)A:①利用三角形的面积公式求出PC的长即可解决问题.注意两解.
②分两种情形讨论即可①P是直角顶点,②O是直角顶点.
B:①利用三角形的面积公式求出PC的长即可解决问题.
②利用两圆一线可得满足条件的点有5个,分别求解即可.
解答 解:(1)把(m,4)代入y=2x+6得2m+6=4,
∴m=-1,
∴C(-1,4),
在Rt△AOB中,OA=3,OB=6,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$.
(2)A:①∵OD⊥CP,
∴S△POC=$\frac{1}{2}$•CP•OD=4,
∵OD=4,CP=2,
∴P1(-3,4),P2(1,4).
②∵∠OCP一定不是直角,
∴当∠OPC=90°时,点P恰好在点D,
∴P1(0,4).
∵直线OC的解析式为y=-4x,
∴直线OP的解析式为y=$\frac{1}{4}$x,
∴y=4时,x=16,
∴P2(16,4).
B:①∵OB⊥CP,
∴S△PAB=$\frac{1}{2}$•CP•OB=6,
∵OB=6,
∴CP=2,
∴P1(-3,4),P2(1,4).
②如图,由图中的两圆一些线可知满足条件的点P坐标为P1(-$\sqrt{29}$-3,4),P2($\sqrt{29}$-3,4),P3(-$\frac{7}{2}$,4),P4($\sqrt{41}$,4),P5(-$\sqrt{41}$,0).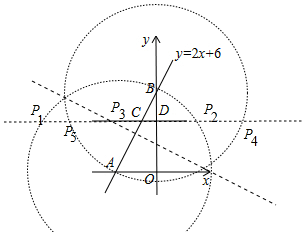
点评 本题考查一次函数综合题、两直线的位置关系、直角三角形的判定和性质、等腰三角形的判定和性质、勾股定理.线段的垂直平分线等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.

| A. | $\frac{1}{2}$x(x+1)=28 | B. | $\frac{1}{2}$x(x-1)=28 | C. | x(x+1)=28 | D. | x(x-1)=28 |
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | | |
| 8 | 9 |
| 15 | 16 |
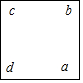
(1)分别用含a的代数式表示b,c,d这三个数:
b=a-7,c=a-8,d=a-1.
(2)求这四个数的和(用含a的代数式表示,要求合并同类项化简);
(3)这四个数的和会等于16吗?如果会,请算出此时a的值;如果不会,说明理由.(要求列方程解答)
 如图,C 为线段 AE 上一动点(不与点 A,E 重合),在 AE 同侧分别作正△ABC 和正△CDE,AD 与 BE 交于点 O,AD 与 BC 交于点 P,BE 与 CD 交于点 Q,连接 PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中正确的结论的个数是( )
如图,C 为线段 AE 上一动点(不与点 A,E 重合),在 AE 同侧分别作正△ABC 和正△CDE,AD 与 BE 交于点 O,AD 与 BC 交于点 P,BE 与 CD 交于点 Q,连接 PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中正确的结论的个数是( )| A. | 2 个 | B. | 3 个 | C. | 4 个 | D. | 5 个 |
| A. | 赚了3元 | B. | 赔了3元 | C. | 不赚不赔 | D. | 赚了30元 |