��Ŀ����
11�� ��ͼ�����߳�Ϊ4�ĵȱ�������AOB������ƽ��ֱ������ϵxOy�У�F��AB���ϵĶ��㣨����˵�A��B�غϣ�������F�ķ���������y=$\frac{k}{x}$��k��0��x��0����OA�߽��ڵ�E������F��FC��x���ڵ�C������EF��OF��
��ͼ�����߳�Ϊ4�ĵȱ�������AOB������ƽ��ֱ������ϵxOy�У�F��AB���ϵĶ��㣨����˵�A��B�غϣ�������F�ķ���������y=$\frac{k}{x}$��k��0��x��0����OA�߽��ڵ�E������F��FC��x���ڵ�C������EF��OF����1����S��OCF=$\sqrt{3}$�����������Ľ���ʽ��
��2���ڣ�1���������£����ж��Ե�EΪԲ�ģ�EA��Ϊ�뾶��Բ��y���λ�ù�ϵ����˵�����ɣ�
��3����AB�����Ƿ���ڵ�F��ʹ��EF��AE�������ڣ������BF��ֵ���������ڣ���˵�����ɣ�
���� ��1����F��x��y�����õ�OC=x��CF=y����ʾ��������OCF����������xy��ֵ����Ϊk��ֵ������ȷ��������������ʽ��
��2����E��EH��ֱ��x�ᣬEG��ֱ��y�ᣬ��OHΪm�����õȱ������ε����ʼ�������Ǻ��������ʾ��EH��OE��������ʾ��E�����꣬���뷴��������ʽ�����m��ֵ��ȷ����EG��OE��EH�ij�������EA��EG�Ĵ�С��ϵ���ɶ���ԲE��y���λ�ù�ϵ�����жϣ�
��3����E��EH��ֱ��x�ᣬ��FB=x�����õȱ������ε����ʼ�������Ǻ��������ʾ��FC��BC��������ʾ��AF��OC����ʾ��AE��OE�ij����ó�OE��EH�ij�����ʾ��E��F���꣬����E��F���ڷ�����ͼ���ϣ��õ���������˻�����г����̣�������̵Ľ�õ�x��ֵ���������BF��FA�ı�ֵ��
��� �⣺��1����F��x��y������x��0��y��0������OC=x��CF=y��
��S��OCF=$\frac{1}{2}$xy=$\sqrt{3}$��
��xy=2 $\sqrt{3}$��
��k=2 $\sqrt{3}$��
�෴������������ʽΪy=$\frac{2\sqrt{3}}{x}$��x��0����
��2����Բ��y�����룬
����Ϊ������E��EH��x�ᣬ����ΪH������E��EG��y�ᣬ����ΪG��
�ڡ�AOB�У�OA=AB=4����AOB=��ABO=��A=60�㣬
��OH=m����tan��AOB=$\frac{EH}{OH}$=$\sqrt{3}$��
��EH=$\sqrt{3}$m��OE=2m��
��E������m��$\sqrt{3}$m����
��E�ڷ�����y=$\frac{2\sqrt{3}}{x}$ͼ���ϣ�
��$\sqrt{3}$m=$\frac{2\sqrt{3}}{m}$��
��m1=$\sqrt{2}$��m2=-$\sqrt{2}$����ȥ����
��OE=2 $\sqrt{2}$��EA=4-2 $\sqrt{2}$��EG=$\sqrt{2}$��
��4-2 $\sqrt{2}$��$\sqrt{2}$��
��EA��EG��
����EΪԲ�ģ�EA��Ϊ�뾶��Բ��y�����룻
��3�����ڣ�
������ڵ�F��ʹAE��FE��
��E����EH��OB�ڵ�H����BF=x��
�ߡ�AOB�ǵȱ������Σ�
��AB=OA=OB=4����AOB=��ABO=��A=60�㣬
��BC=FB•cos��FBC=$\frac{1}{2}$x��FC=FB•sin��FBC=$\frac{\sqrt{3}}{2}$x��
��AF=4-x��OC=OB-BC=4-$\frac{1}{2}$x��
��AE��FE��
��AE=AF•cosA=2-$\frac{1}{2}$x��
��OE=OA-AE=$\frac{1}{2}$x+2��
��OH=OE•cos��AOB=$\frac{1}{4}$x+1��EH=OE•sin��AOB=$\frac{\sqrt{3}}{4}$x+$\sqrt{3}$��
��E�� $\frac{1}{4}$x+1��$\frac{\sqrt{3}}{4}$x+$\sqrt{3}$����F��4-$\frac{1}{2}$x��$\frac{\sqrt{3}}{2}$x����
��E��F����˫����y=$\frac{k}{x}$��ͼ���ϣ�
�ࣨ $\frac{1}{4}$x+1���� $\frac{\sqrt{3}}{4}$x+$\sqrt{3}$��=��4-$\frac{1}{2}$x��•$\frac{\sqrt{3}}{2}$x��
��ã�x1=4��x2=$\frac{4}{5}$��
��F��AB���ϵĶ��㣨����˵�A��B�غϣ���
��x=4�������⣬
��BF=$\frac{4}{5}$ʱ��EF��AE��
���� �������ڷ����������ۺ��⣬�漰��֪ʶ�У�������������ͼ�������ʣ�������ͼ�����ʣ��ȱ������ε����ʣ�������Ǻ������壬�������շ�����������ͼ���������ǽⱾ��Ĺؼ���

| A�� | $\frac{1}{2}$x��x+1��=28 | B�� | $\frac{1}{2}$x��x-1��=28 | C�� | x��x+1��=28 | D�� | x��x-1��=28 |
| �� | һ | �� | �� | �� | �� | �� |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | | |
| 8 | 9 |
| 15 | 16 |
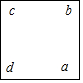
��1���ֱ��ú�a�Ĵ���ʽ��ʾb��c��d����������
b=a-7��c=a-8��d=a-1��
��2�������ĸ����ĺͣ��ú�a�Ĵ���ʽ��ʾ��Ҫ��ϲ�ͬ�����
��3�����ĸ����ĺͻ����16������ᣬ�������ʱa��ֵ��������ᣬ˵�����ɣ���Ҫ���з��̽��
 ��ͼ����ACD�ǡ�ABC����ǣ���ABC��ƽ�������ACD��ƽ���߽��ڵ�A1����A1BC��ƽ�������A1CD��ƽ���߽��ڵ�A2��������An-1BC��ƽ�������An-1CD��ƽ���߽��ڵ�An�����A=�ȣ���
��ͼ����ACD�ǡ�ABC����ǣ���ABC��ƽ�������ACD��ƽ���߽��ڵ�A1����A1BC��ƽ�������A1CD��ƽ���߽��ڵ�A2��������An-1BC��ƽ�������An-1CD��ƽ���߽��ڵ�An�����A=�ȣ���