题目内容
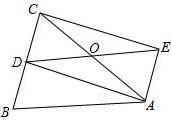
 如图,AB=DC,AC=DB,AC与BD交于点O,求证:
如图,AB=DC,AC=DB,AC与BD交于点O,求证:(1)△ABC≌△DCB;
(2)OA=OD;
(3)∠ABD=∠DCA.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)根据SSS,可得证明结论;
(2)根据全等三角形的性质,可得对应边相等,对应角相等,根据AAS,可得△OAB与△ODC的关系,根据全等三角形的性质,可得证明的结论;
(3)根据△ABO≌△DCO,△证明结论.
(2)根据全等三角形的性质,可得对应边相等,对应角相等,根据AAS,可得△OAB与△ODC的关系,根据全等三角形的性质,可得证明的结论;
(3)根据△ABO≌△DCO,△证明结论.
解答:证明:(1)在△ABC和△DCB中,
,
∴△ABC≌△DCB(SSS);
(2)∵△ABC≌△DCB,
∴∠A=∠D,AB=DC.
∵∠AOB与∠DOC是对顶角,
∴∠AOB=∠DOC.
在△ABO和△DCO中,
,
∴△AOB≌△DOC(AAS)
AO=DO;
(3)∵△AOB≌△DOC,
∴∠ABD=∠DCA.
|
∴△ABC≌△DCB(SSS);
(2)∵△ABC≌△DCB,
∴∠A=∠D,AB=DC.
∵∠AOB与∠DOC是对顶角,
∴∠AOB=∠DOC.
在△ABO和△DCO中,
|
∴△AOB≌△DOC(AAS)
AO=DO;
(3)∵△AOB≌△DOC,
∴∠ABD=∠DCA.
点评:本题考查了全等三角形的判定与性质,利用了SSS、AAS证明三角形全等,利用了全等三角形的对应边相等、对应角相等.

练习册系列答案
相关题目
根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g)两种产品的销售数量比为2:5,每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?设应该分装大小瓶两种产品x瓶、y瓶,则可用二元一次方程组表示题中的数量关系为( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 在△ABC中,AB=AC,D为BC的中点,四边形ABDE是平行四边形.
在△ABC中,AB=AC,D为BC的中点,四边形ABDE是平行四边形. 如图,△ABC中,∠ABC的平分线与△ABC的外角∠DAC、∠ACF的平分线相交于点E,EH⊥AC,垂足为点H.求证:∠AEB=∠CEH.
如图,△ABC中,∠ABC的平分线与△ABC的外角∠DAC、∠ACF的平分线相交于点E,EH⊥AC,垂足为点H.求证:∠AEB=∠CEH.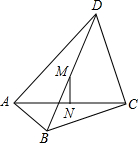 如图,四边形ABCD中,∠BAD=∠BCD=90°,M、N分别是对角线BD、AC的中点.求证:直线MN是线段AC的垂直平分线.
如图,四边形ABCD中,∠BAD=∠BCD=90°,M、N分别是对角线BD、AC的中点.求证:直线MN是线段AC的垂直平分线.