题目内容
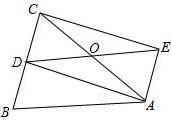 在△ABC中,AB=AC,D为BC的中点,四边形ABDE是平行四边形.
在△ABC中,AB=AC,D为BC的中点,四边形ABDE是平行四边形.(1)求证:四边形ADCE是矩形;
(2)若AC、DE交于点O,四边形ADCE的面积为16
| 3 |
(3)当△ABC满足什么条件时,矩形ADCE是正方形,并说明理由.
考点:矩形的判定,平行四边形的性质,正方形的判定
专题:
分析:(1)已知四边形ABDE是平行四边形,只需证得它的一个内角是直角即可;在等腰△ABC中,AD是底边的中线,根据等腰三角形三线合一的性质即可证得∠ADC是直角,由此得证;
(2)根据矩形的性质得出AD的长度,进而得出∠DAC=30°即可求出答案;
(3)当满足条件AC=BC,证明CD⊥AB且相等即可.
(2)根据矩形的性质得出AD的长度,进而得出∠DAC=30°即可求出答案;
(3)当满足条件AC=BC,证明CD⊥AB且相等即可.
解答:证明:(1)∵四边形ABDE是平行四边形,
∴AE∥BC,AB=DE,AE=BD.
∵D为BC中点,
∴CD=BD.
∴CD∥AE,CD=AE.
∴四边形ADCE是平行四边形.
∵AB=AC,D为BC中点,
∴AD⊥BC,即∠ADC=90°,
∴平行四边形ADCE是矩形;
(2)解:∵平行四边形ADCE是矩形,四边形ADCE的面积为16
,CD=4,
∴AD•CD=4AD=16
,DO=AO=CO=EO,
解得:AD=4
,
∴tan∠DAC=
=
=
,
∴∠DAC=30°,
∴∠ODA=30°,
∴∠AOD=120°.
(3)当满足条件AC=BC.
证明:∵AC=BC,D为AB中点,
∴CD⊥AB(三线合一的性质),即∠ADC=90°.
∵四边形BCED为平行四边形,四边形ADCE为平行四边形,
∴DE=BC=AC,∠AFD=∠ACB=90°.
∴四边形ADCE为正方形.(对角线互相垂直且相等的四边形是正方形)
∴AE∥BC,AB=DE,AE=BD.
∵D为BC中点,
∴CD=BD.
∴CD∥AE,CD=AE.
∴四边形ADCE是平行四边形.
∵AB=AC,D为BC中点,
∴AD⊥BC,即∠ADC=90°,
∴平行四边形ADCE是矩形;
(2)解:∵平行四边形ADCE是矩形,四边形ADCE的面积为16
| 3 |
∴AD•CD=4AD=16
| 3 |
解得:AD=4
| 3 |
∴tan∠DAC=
| CD |
| AD |
| 4 | ||
4
|
| ||
| 3 |
∴∠DAC=30°,
∴∠ODA=30°,
∴∠AOD=120°.
(3)当满足条件AC=BC.
证明:∵AC=BC,D为AB中点,
∴CD⊥AB(三线合一的性质),即∠ADC=90°.
∵四边形BCED为平行四边形,四边形ADCE为平行四边形,
∴DE=BC=AC,∠AFD=∠ACB=90°.
∴四边形ADCE为正方形.(对角线互相垂直且相等的四边形是正方形)
点评:本题主要考查正方形的判定、菱形的判定与性质和勾股定理等知识点,此题是道综合体,有一定的难度,解答的关键还是要能熟练掌握各种四边形的基本性质.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
下列图形中,不是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
圆柱的底面半径为1,高为2,则该圆柱体的表面积为( )
| A、π | B、2π | C、4π | D、6π |
 如图,点A在双曲线
如图,点A在双曲线 如图,已知AD=BC,∠C=∠D,求证:△ABD≌△BAC.
如图,已知AD=BC,∠C=∠D,求证:△ABD≌△BAC. 如图,AB=DC,AC=DB,AC与BD交于点O,求证:
如图,AB=DC,AC=DB,AC与BD交于点O,求证: