题目内容
19. 将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=70°,则∠1=40 度;△EFG是等腰 三角形.
将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=70°,则∠1=40 度;△EFG是等腰 三角形.
分析 根据翻折变换的性质求出∠GEF的度数,从而求出∠GEB的度数,再根据平行线的性质求出∠1;根据AD∥BC得到∠GFE=∠FEC,根据翻折不变性得到∠GEF=∠GFE,由等角对等边得到GE=GF.
解答 解:∵∠GEF=∠FEC=70°,
∴∠BEG=180°-70°×2=40°,
∵AD∥BC,
∴∠1=∠BEG=40°;
∵AD∥BC,
∴∠GFE=∠FEC,
∴∠GEF=∠GFE,
∴GE=GF,
∴△EFG是等腰三角形.
故答案为:40,等腰.
点评 本题考查的是图形翻折变换的性质及等腰三角形的判定定理,熟知图形翻折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
9.某中学七年级共400人,在期末统考后对本次考试中数学测验情况进行抽样了解,下列抽取的样本最合理的是( )
| A. | 抽取前50名同学的数学成绩 | |
| B. | 抽取后50名同学的数学成绩 | |
| C. | 抽取5班同学的数学成绩 | |
| D. | 抽取各班学好为5的倍数的同学的数学成绩 |
10.一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表:
(1)求这个二次函数的表达式;
(2)求m的值.
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{7}{2}$ | 0 | $\frac{5}{2}$ | 4 | $\frac{9}{2}$ | 4 | m | 0 | … |
(2)求m的值.
4. 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:
如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:
根据上表解决下面这个实际问题:姚明的身高是226厘米,可预测他的指距约为( )
 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:
如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:| 指距d(cm) | 20 | 21 | 22 | 23 |
| 身高h(cm) | 160 | 169 | 178 | 187 |
| A. | 25.3厘米 | B. | 26.3厘米 | C. | 27.3厘米 | D. | 28.3厘米 |
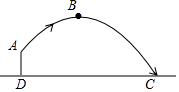 体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为4m时,达到最大高度4m的B处(如图),问该学生把实心球扔出多远?(结果保留根号)
体育测试时,九年级一名学生,双手扔实心球.已知实心球所经过的路线是某个二次函数图象的一部分,如果球出手处A点距离地面的高度为2m,当球运行的水平距离为4m时,达到最大高度4m的B处(如图),问该学生把实心球扔出多远?(结果保留根号)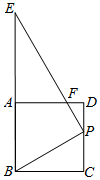 如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.
如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.