题目内容
8.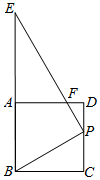 如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.
如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.(1)图中与Rt△BCP相似的三角形共有3个,分别是Rt△EPB,Rt△PDF,Rt△EAF;
(2)请选择第(1)问答案中的任意一个三角形,完成该三角形与△BCP相似的证明.
分析 (1)根据相似三角形的判定定理得到Rt△EPB,Rt△PDF,Rt△EAF均与Rt△BCP相似;
(2)Rt△BCP∽Rt△EPB.利用“两角法”证得结论即可.
解答 解:(1)图中与Rt△BCP相似的三角形共有 3个,分别是 Rt△EPB,Rt△PDF,Rt△EAF;
故答案是:3;Rt△EPB,Rt△PDF,Rt△EAF;
(2)答案不唯一,如:
∵四边形ABCD是正方形,
∴∠ABP+∠PBC=∠C=90°.
∵∠PBC+∠BPC=90°,
∴∠ABP=∠BPC.
又∵∠BPE=∠C=90°,
∴Rt△BCP∽Rt△EPB.
点评 本题考查了相似三角形的判定,正方形的性质.相似三角形的判定方法:
(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;(4)两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
18.直四棱柱、长方体和正方体之间的包含关系是( )
| A. |  | B. |  | C. |  | D. |  |
16.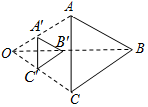 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )| A. | 1:3 | B. | 1:4 | C. | 1:8 | D. | 1:9 |
13.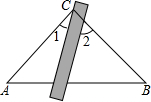 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=67°,则∠1的度数为( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=67°,则∠1的度数为( )
 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=67°,则∠1的度数为( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上,若∠2=67°,则∠1的度数为( )| A. | 33° | B. | 23° | C. | 67° | D. | 无法确定 |
 将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=70°,则∠1=40 度;△EFG是等腰 三角形.
将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=70°,则∠1=40 度;△EFG是等腰 三角形.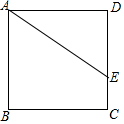 如图,正方形ABCD中,点E在DC边上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC的长为2或10.
如图,正方形ABCD中,点E在DC边上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC的长为2或10. 如图,?ABCD中,点E,F分别在BC,AD上,且AE平分∠BAD,BF平分∠ABC,求证:CE=DE.
如图,?ABCD中,点E,F分别在BC,AD上,且AE平分∠BAD,BF平分∠ABC,求证:CE=DE.