题目内容
11.已知m,n为实数,且m=$\sqrt{{n}^{2}-9}+\sqrt{9-{n}^{2}}$+4,则m-n=1或7.分析 根据题目中的式子可以求得m、n的值,从而可以求得m-n的值.
解答 解:∵m=$\sqrt{{n}^{2}-9}+\sqrt{9-{n}^{2}}+4$,
∴$\left\{\begin{array}{l}{{n}^{2}-9≥0}\\{9-{n}^{2}≥0}\end{array}\right.$,
解得,n=-3或n=3,
∴m=4,
∴当m=4,n=-3时,m-n=4-(-3)=7,
当m=4,n=3时,m-n=4-3=1,
故答案为:1或7.
点评 本题考查二次根似的化简求值,解题的关键是明确二次根式的意义.

练习册系列答案
相关题目
1.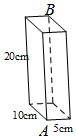 如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )
如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )
 如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )
如图,长方体的长为10cm,宽为5cm,高为20cm.若一只蚂蚁沿着长方体的表面从点A爬到点B,需要爬行的最短路径是( )| A. | 20+5$\sqrt{5}$ | B. | 25 | C. | 10$\sqrt{5}$+5 | D. | $5\sqrt{21}$ |
2.用反证法证明命题“三角形中至少有一个角大于或等于60°”时,首先应假设这个三角形中( )
| A. | 有一个内角大于60° | B. | 有一个内角小于60° | ||
| C. | 每一个内角都大于60° | D. | 每一个内角都小于60° |
16.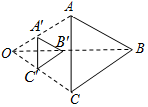 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )| A. | 1:3 | B. | 1:4 | C. | 1:8 | D. | 1:9 |
 将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=70°,则∠1=40 度;△EFG是等腰 三角形.
将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=70°,则∠1=40 度;△EFG是等腰 三角形.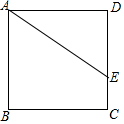 如图,正方形ABCD中,点E在DC边上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC的长为2或10.
如图,正方形ABCD中,点E在DC边上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC的长为2或10. 如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上一点,BE=DF.
如图,正方形ABCD的边长是4,E是AB上一点,F是AD延长线上一点,BE=DF.