题目内容
5.计算:$\frac{1}{3}\sqrt{27{a}^{3}}-{a}^{2}\sqrt{\frac{3}{a}}+3a\sqrt{\frac{a}{3}}-\frac{a}{4}\sqrt{108a}$.分析 首先化简二次根式,进而合并求出答案.
解答 解:$\frac{1}{3}\sqrt{27{a}^{3}}-{a}^{2}\sqrt{\frac{3}{a}}+3a\sqrt{\frac{a}{3}}-\frac{a}{4}\sqrt{108a}$
=$\frac{1}{3}$×3a$\sqrt{3a}$-a2×$\frac{\sqrt{3a}}{a}$+3a×$\frac{\sqrt{3a}}{3}$-$\frac{a}{4}$×$6\sqrt{3a}$
=a$\sqrt{3a}$-a$\sqrt{3a}$+a$\sqrt{3a}$-$\frac{3a}{2}$$\sqrt{3a}$
=-$\frac{a}{2}$$\sqrt{3a}$.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
15.一直角三角形的两直角边长为3和4,则第三边长为( )
| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{7}$或5 | D. | 7 |
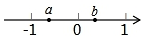 有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是2.
有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是2.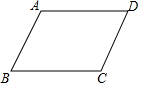 如图,如果∠B=65°,AD∥BC,AB∥DC,那么∠A=115°;∠D=65°;∠B=∠D.
如图,如果∠B=65°,AD∥BC,AB∥DC,那么∠A=115°;∠D=65°;∠B=∠D.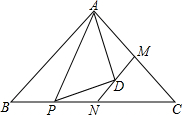 如图,等腰直角三角形ABC,斜边上一动点P,连接AP,以AP为斜边作等腰直角三角形,顶点为D,点M是AC边中点,连接MD,延长交斜边于点N,求证:BN=CN.
如图,等腰直角三角形ABC,斜边上一动点P,连接AP,以AP为斜边作等腰直角三角形,顶点为D,点M是AC边中点,连接MD,延长交斜边于点N,求证:BN=CN.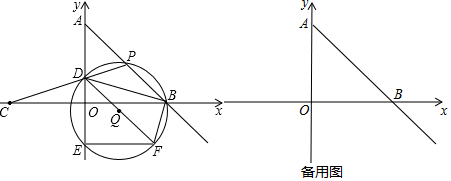
 (1)解不等式$\frac{x-2}{2}$-(x-1)<1.并把解在数轴上表示出来.
(1)解不等式$\frac{x-2}{2}$-(x-1)<1.并把解在数轴上表示出来.