题目内容
13.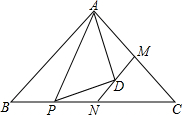 如图,等腰直角三角形ABC,斜边上一动点P,连接AP,以AP为斜边作等腰直角三角形,顶点为D,点M是AC边中点,连接MD,延长交斜边于点N,求证:BN=CN.
如图,等腰直角三角形ABC,斜边上一动点P,连接AP,以AP为斜边作等腰直角三角形,顶点为D,点M是AC边中点,连接MD,延长交斜边于点N,求证:BN=CN.
分析 延长AD到E,交BC于F,使得AD=DE连接CE、PE,得到△APE是等腰直角三角形,根据三角形的中位线的性质得到DM∥CE,推出点A,P,E,C四点共圆,根据圆周角定理得到∠ACP=∠ECP=45°,得到CE⊥AC,NM⊥AC,证得NM∥AB于是得到结论.
解答 解: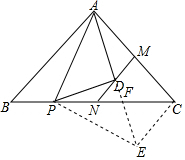 延长AD到E,交BC于F,使得AD=DE连接CE、PE,
延长AD到E,交BC于F,使得AD=DE连接CE、PE,
∵△ADP是等腰直角三角形,
∴△APE是等腰直角三角形,
∵M是AC中点,
∴DM∥CE,
∵∠APC=45°+∠CPD=45°+∠BAP,
∴∠CPD=∠BAP,
∵∠BAP+∠CAD=∠CPE+∠CPD=45°,
∴∠CPE=∠CAD,
∵∠AFC=∠PFE,
∴点A,P,E,C四点共圆,
∴∠ACP=∠ECP=45°,
∴∠ACE=∠ACP+∠ECP=90°,
∴CE⊥AC,NM⊥AC,
∵AB⊥AC
∴NM∥AB
∴N为BC中点,BN=CN.
点评 本题考查了等腰直角三角形的判定和性质,三角形中位线的性质,四点共圆,正确作出辅助线是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
3.一个物体由多个完全相同的小正方形组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为( )


| A. | 4 | B. | 5 | C. | 8 | D. | 10 |
8.正方形ABCD的对角线AC的长是12cm,则边长AB的长是( )
| A. | 6$\sqrt{2}$ | B. | 2$\sqrt{12}$ | C. | 6 | D. | 8 |
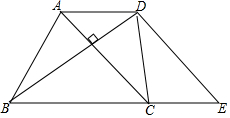 如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD,
如图,在四边形ABCD中,AD∥BC,且AD<BC,AC、BD为两条对角线,且AC⊥BD,AC=BD, 在数轴上的点A,B位置如图所示,若数轴上的点C到点A与点B的距离之和为8.求点C表示的数.
在数轴上的点A,B位置如图所示,若数轴上的点C到点A与点B的距离之和为8.求点C表示的数.