题目内容
12．某种品牌毛巾原零售价每条6元，凡一次性购买两条以上（含两条），商家推出两种优惠销售办法，第一种：“两条按原价，其余按七折优惠”；第二种：“全部按原价的八折优惠”，若想在购买相同数量的情况下，要使第一种办法比第二种办法得到的优惠多，最少要购买几条毛巾？分析 设购买x条毛巾，根据两种不同计费方式列出不等式求解即可．
解答 解：设购买x条毛巾，由题意可得：
2×6+6×0.7（x-2）＜6×0.8x，
解得：x＞6，
∵x为正整数，
∴x最小值是7，
答：若想在购买相同数量的情况下，要使第一种办法比第二种办法得到的优惠多，最少要购买7条毛巾．
点评 本题主要考查一元一次不等式的应用，根据题意得出不等关系并列出不等式是解题的关键．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
2．
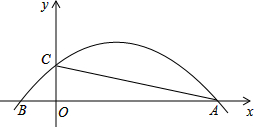如图，抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A，B两点，与y轴交于点C．若点P是线段AC上方的抛物线上一动点，当△ACP的面积取得最大值时，点P的坐标是（ ）
如图，抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A，B两点，与y轴交于点C．若点P是线段AC上方的抛物线上一动点，当△ACP的面积取得最大值时，点P的坐标是（ ）| A． | （4，3） | B． | （5，$\frac{35}{12}$） | C． | （4，$\frac{35}{12}$） | D． | （5，3） |
3．连接A、B两地的高速公路全长为420km，一辆小汽车和一辆客车分别从A、B两地同时出发，相向而行，经过2.5h相遇，相遇时，小汽车比客车多行驶了70km，若设小汽车和客车的平均速度分别为xkm/h和ykm/h，则下列方程组正确的是（ ）
| A． | $\left\{\begin{array}{l}{2.5x+2.5y=420}\\{2.5x-2.5y=70}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x-y=70}\\{2.5x+2.5y=420}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=70}\\{2.5x+2.5y=420}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=70}\\{2.5x-2.5y=420}\end{array}\right.$ |
17．下列各命题中，是真命题的是（ ）
| A． | 同位角相等 | |
| B． | 和为180°的两个角互为邻补角 | |
| C． | 经过直线外一点，有且只有一条直线与这条直线平行 | |
| D． | 相等的角是对顶角 |
甲、乙两车从A城出发前往B城，在整个行程中，两车离开A城的距离y与t的对应关系如图所示：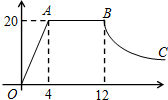
某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种．如图是某天大棚内温度y（℃）随时间x（小时）变化的函数图象，其中OA段是系统开启后的升温阶段，y与x成正比例，BC段是系统关闭后的降温阶段，y与x成反比例．请根据图中信息解答下列问题：