题目内容
17.下列计算正确的是( )| A. | (x4)3=x12 | B. | a2•a5=a10 | C. | (3a)2=6a2 | D. | a6÷a2=a3 |
分析 分别利用同底数幂的乘除运算法则以及积的乘方运算法则分别化简求出答案.
解答 解:A、(x4)3=x12,正确;
B、a2•a5=a7,故此选项错误;
C、(3a)2=9a2,故此选项错误;
D、a6÷a2=a4,故此选项错误;
故选:A.
点评 此题主要考查了同底数幂的乘除运算法则以及积的乘方运算等知识,正确掌握运算法则是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.函数y=$\frac{2}{x+1}$的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
12.东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为p=$\left\{\begin{array}{l}{\frac{1}{4}t+30(1≤t≤24,t为整数)}\\{-\frac{1}{2}t+48(25≤t≤48,t为整数)}\end{array}\right.$,且其日销售量y(kg)与时间t(天)的关系如表:
(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
| 时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
2.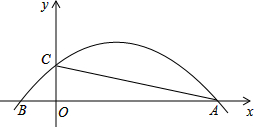 如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
 如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )| A. | (4,3) | B. | (5,$\frac{35}{12}$) | C. | (4,$\frac{35}{12}$) | D. | (5,3) |
6.点P(-2,-3)向右平移2个单位,再向下平移3个单位,则所得到的点的坐标为( )
| A. | (0,0) | B. | (-4,0) | C. | (0,-6) | D. | (0,6) |
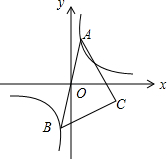 如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.
如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.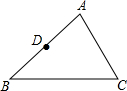 如图,已知△ABC中,D为AB的中点.
如图,已知△ABC中,D为AB的中点.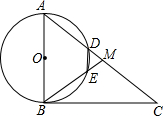 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.