题目内容
14.给出一种运算:对于函数y=xn,规定y′=nxn-1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是( )| A. | x1=4,x2=-4 | B. | x1=2,x2=-2 | C. | x1=x2=0 | D. | x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$ |
分析 首先根据新定义求出函数y=x3中的n,再与方程y′=12组成方程组得出:3x2=12,用直接开平方法解方程即可.
解答 解:由函数y=x3得n=3,则y′=3x2,
∴3x2=12,
x2=4,
x=±2,
x1=2,x2=-2,
故选B.
点评 本题考查了利用直接开平方法解一元二次方程,同时还以新定义的形式考查了学生的阅读理解能力;注意:①二次项系数要化为1,②根据平方根的意义开平方时,是两个解,且是互为相反数,不要丢解.

练习册系列答案
相关题目
4.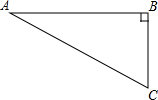 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
5.函数y=$\frac{2}{x+1}$的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
2.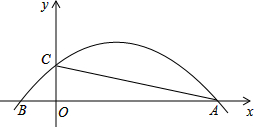 如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
 如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )| A. | (4,3) | B. | (5,$\frac{35}{12}$) | C. | (4,$\frac{35}{12}$) | D. | (5,3) |
6.点P(-2,-3)向右平移2个单位,再向下平移3个单位,则所得到的点的坐标为( )
| A. | (0,0) | B. | (-4,0) | C. | (0,-6) | D. | (0,6) |
3.连接A、B两地的高速公路全长为420km,一辆小汽车和一辆客车分别从A、B两地同时出发,相向而行,经过2.5h相遇,相遇时,小汽车比客车多行驶了70km,若设小汽车和客车的平均速度分别为xkm/h和ykm/h,则下列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{2.5x+2.5y=420}\\{2.5x-2.5y=70}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-y=70}\\{2.5x+2.5y=420}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=70}\\{2.5x+2.5y=420}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=70}\\{2.5x-2.5y=420}\end{array}\right.$ |
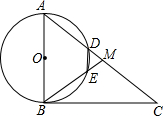 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E. 甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示:
甲、乙两车从A城出发前往B城,在整个行程中,两车离开A城的距离y与t的对应关系如图所示: