题目内容
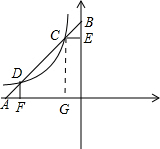
 如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=-
如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=-| 5 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:反比例函数综合题
专题:
分析:①根据函数值与相应自变量的关系,可得C点坐标,根据待定系数法,可得一次函数解析式,可得答案;
②根据解方程组,可得C、D点的坐标,根据全等三角形的判定与性质,可得答案;
③根据图形的分割,可得梯形、矩形,根据面积的和差,可得答案
④根据函数与不等式的关系:函数图象在上方的函数值大,可得答案
②根据解方程组,可得C、D点的坐标,根据全等三角形的判定与性质,可得答案;
③根据图形的分割,可得梯形、矩形,根据面积的和差,可得答案
④根据函数与不等式的关系:函数图象在上方的函数值大,可得答案
解答:解:①由反比例函数y2=-
(x<0)经过C,点C的横坐标为-1,得
y=-
=5,即C(-1,5).
反比例函数与一次函数交于C、D点,
5=-1+b,解得b=6,故①正确;
②CE⊥y轴于E点,E(0,-5),BE=6-5=1.
反比例函数与一次函数交于C、D点,联立
,
x2+6x+5=0
解得x1=-5,x2=-1,当x=-5时,y=-5+6=1,即D(-5,1),即DF=1,
在△ADF和△CBE中,
,
△ADF≌△CBE(AAS),AD=BC,故②正确;
③作CG⊥x轴.,
S△CDFOE=S梯形DFGC+S矩形CGOE
=
+OG•CG
+1×5=17,故③错误;
④由一次函数图象在反比例函数图象上方的部分,得-5<x<-1,
即当-5<x<-1时,y1>y2,故④错误;
故选:B.
| 5 |
| x |
y=-
| 5 |
| -1 |
反比例函数与一次函数交于C、D点,
5=-1+b,解得b=6,故①正确;
②CE⊥y轴于E点,E(0,-5),BE=6-5=1.
反比例函数与一次函数交于C、D点,联立
|
x2+6x+5=0
解得x1=-5,x2=-1,当x=-5时,y=-5+6=1,即D(-5,1),即DF=1,
在△ADF和△CBE中,

|
△ADF≌△CBE(AAS),AD=BC,故②正确;
③作CG⊥x轴.,
S△CDFOE=S梯形DFGC+S矩形CGOE
=
| (DF+CG)FG |
| 2 |
| (1+5)×4 |
| 2 |
④由一次函数图象在反比例函数图象上方的部分,得-5<x<-1,
即当-5<x<-1时,y1>y2,故④错误;
故选:B.
点评:本题考查了反比例函数综合题,利用了自变量与函数值的对应关系,点的坐标与函数解析式的关系,全等三角形的判定与性质,图形分割法求图形的面积,函数图象与不等式的关系.

练习册系列答案
相关题目
从一块长30cm,宽12cm的长方形薄铁皮的四个角上,截去四个相同的小正方形,余下部分的面积为296cm2,则截去小正方形的边长为( )
| A、1cm | B、2cm |
| C、3cm | D、4cm |
 如图,在五边形ABCDE中,AB∥DE,若△ABE的面积为5,则△ABD的面积为( )
如图,在五边形ABCDE中,AB∥DE,若△ABE的面积为5,则△ABD的面积为( )| A、4 | B、5 | C、10 | D、无法判断 |
 已知抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线x=
已知抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线x= 如图,取一张正方形纸片ABCD四条边的中点E,F,G,H,连结AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的边长为
如图,取一张正方形纸片ABCD四条边的中点E,F,G,H,连结AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的边长为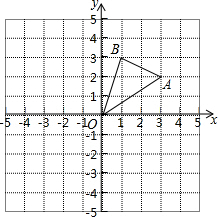 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).将△AOB绕点O逆时针旋转90°后得到△A1OB1.
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).将△AOB绕点O逆时针旋转90°后得到△A1OB1.