题目内容
 如图,取一张正方形纸片ABCD四条边的中点E,F,G,H,连结AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的边长为
如图,取一张正方形纸片ABCD四条边的中点E,F,G,H,连结AF,BG,CH,DE.沿这些连线剪4刀,便剪出中间这个较小的正方形(阴影部分).请试一试,若要剪出的小正方形的边长为| 5 |
考点:图形的剪拼
专题:
分析:设BG与AF的交点为M,由于BE=DG,且BE∥DG,易证得四边形BEDG是平行四边形,即DE∥BG,结合三角形中位线定理,可用小正方形的边长表示出Rt△ABM两条直角边的长,进而可用小正方形的边长表示出正方形的面积,由此求得正方形纸片ABCD的边长.
解答:解:如图;
易知BE=DG,且BE∥DG,
∴四边形BEDG是平行四边形,即DE∥BG;
又E是AB中点,所以EN是△ABM的中位线,
∴MN=
AM,同理可得MQ=BM=
BQ;
∵小正方形的边长为
cm,
∴AM=DN=CP=BQ=2
,BM=AN=PD=CQ=
cm;
∴S正方形ABCD=S△ABM+S△AND+S△CPD+S△BQC+S正方形MNPQ
=
2+
2+
2+
2+
2=25cm2,
∴正方形纸片ABCD的边长=5cm,
故答案为:5.

易知BE=DG,且BE∥DG,
∴四边形BEDG是平行四边形,即DE∥BG;
又E是AB中点,所以EN是△ABM的中位线,
∴MN=
| 1 |
| 2 |
| 1 |
| 2 |
∵小正方形的边长为
| 5 |
∴AM=DN=CP=BQ=2
| 5 |
| 5 |
∴S正方形ABCD=S△ABM+S△AND+S△CPD+S△BQC+S正方形MNPQ
=
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
∴正方形纸片ABCD的边长=5cm,
故答案为:5.
点评:此题主要考查了正方形的性质、图形面积的求法以及三角形中位线定理的综合应用,难度不大.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=-
如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=-| 5 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
36的平方根( )
| A、±4 | B、±6 | C、6 | D、4 |
某工程需在规定日期内完成,若甲工程队独做,恰好如期完成,如果乙工程队独做,则超过规定日期3天完成,现在甲、乙两队合作2天,剩下的由乙队独做,恰好在规定日期完成,求规定日期,如果设规定日期为x天,则下列正确( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
黄河农场各用10块面积相同的试验田种植甲、乙两种麦子,收获后对两种麦子产量(单位:吨/亩)的数据统计如下:
甲=0.61,
乙=0.59,S甲2=0.01,S乙2=0.002,则由上述数据推断乙种麦子产量比较稳定的依据是( )
. |
| x |
. |
| x |
A、
| ||||
| B、S甲2>S乙2 | ||||
C、
| ||||
D、
|
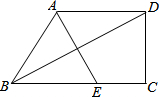 如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是
如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是