题目内容
 已知抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线x=
已知抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线x=| 5 |
| 2 |
(1)求此抛物线解析式和顶点P坐标;
(2)求证:∠ODB=∠OAD;
(3)设直线AD与抛物线的对称轴交于点M,点N在x轴上,若△AMP与△BND相似,求点N坐标.
考点:二次函数综合题
专题:压轴题
分析:(1)利用直线解析式求出点A、D,然后求出点C的坐标,根据对称轴求出点B的坐标,然后利用待定系数法求二次函数解析式解答;
(2)求出∠ODB和∠OAD的正切值,然后根据等角的正切值相等证明;
(3)先求出点M的坐标,再求出∠AMP=∠OBD,然后求出AM、PM、BD,再根据相似三角形对应边成比例,分两种情况讨论求出BN,再求出ON,最后写出点N的坐标即可.
(2)求出∠ODB和∠OAD的正切值,然后根据等角的正切值相等证明;
(3)先求出点M的坐标,再求出∠AMP=∠OBD,然后求出AM、PM、BD,再根据相似三角形对应边成比例,分两种情况讨论求出BN,再求出ON,最后写出点N的坐标即可.
解答:(1)解:∵直线y=-2x+2与x轴交于点A,与y轴交于点D,
∴A(1,0),D(0,2),
∵D为OC中点,
∴C(0,4),
∵A(1,0),对称轴为直线x=
,
∴B(4,0),
∵抛物线y=ax2+bx+c经过A、B、C点,
∴
,
解得
,
∴此抛物线的解析式为y=x2-5x+4,
顶点P的坐标为(
,-
);
(2)证明:在Rt△AOD和Rt△ACD中,∠DOB=90°,
∴tan∠ODB=
=
=2,tan∠OAD=
=
=2,
∴∠ODB=∠OAD;
(3)解:∵直线AD与抛物线的对称轴交于点M,对称轴为直线x=
,
∴M(
,-3),
∵∠ODB=∠OAD,
∴∠ADO=∠OBD,
∵对称轴平行于y轴,
∴∠ADO=∠AMP,
∴∠AMP=∠OBD,
∵AM=
=
,PM=-
-(-3)=
,BD=
=2
,
∴N点在点B左侧,可有△AMP∽△DBN或△AMP∽△NBD,
∴
=
或
=
,
∴
=
或
=
,
解得BN=1或BN=20,
∴ON=4-1=3或ON=20-4=16,
∴N(3,0)或(-16,0).
∴A(1,0),D(0,2),
∵D为OC中点,
∴C(0,4),
∵A(1,0),对称轴为直线x=
| 5 |
| 2 |
∴B(4,0),
∵抛物线y=ax2+bx+c经过A、B、C点,
∴
|
解得
|
∴此抛物线的解析式为y=x2-5x+4,
顶点P的坐标为(
| 5 |
| 2 |
| 9 |
| 4 |
(2)证明:在Rt△AOD和Rt△ACD中,∠DOB=90°,
∴tan∠ODB=
| OB |
| OD |
| 4 |
| 2 |
| OD |
| OA |
| 2 |
| 1 |

∴∠ODB=∠OAD;
(3)解:∵直线AD与抛物线的对称轴交于点M,对称轴为直线x=
| 5 |
| 2 |
∴M(
| 5 |
| 2 |
∵∠ODB=∠OAD,
∴∠ADO=∠OBD,
∵对称轴平行于y轴,
∴∠ADO=∠AMP,
∴∠AMP=∠OBD,
∵AM=
(
|
3
| ||
| 2 |
| 9 |
| 4 |
| 3 |
| 4 |
| 22+42 |
| 5 |
∴N点在点B左侧,可有△AMP∽△DBN或△AMP∽△NBD,
∴
| AM |
| DB |
| PM |
| BN |
| AM |
| BN |
| PM |
| BD |
∴
| ||||
2
|
| ||
| BN |
| ||||
| BN |
| ||
2
|
解得BN=1或BN=20,
∴ON=4-1=3或ON=20-4=16,
∴N(3,0)或(-16,0).
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,锐角三角函数,勾股定理,相似三角形的判定与性质,难点在于(3)要分情况讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列从左到右的变形是因式分解的是( )
| A、(x+1)(x+3)=x2+4x+3 |
| B、x2-2x+1=x(x-2)+1 |
| C、a2-9=(a+3)(a-3) |
| D、2x(a+b)=2ax+2bx |
老师给出:a+b=2,a2+b2=2,你能计算出ab的值为( )
| A、0 | ||
B、-
| ||
| C、-1 | ||
| D、1 |
 如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=-
如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=-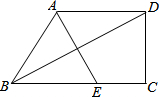 如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是
如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是