题目内容
1.解方程:(1)$\frac{4x-1}{x-2}$-2=$\frac{1}{4-2x}$
(2)$\frac{x-2}{x+2}$-$\frac{16}{{x}^{2}-4}$=1.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)两边同乘以2x-4得:2(4x-1)-2(2x-4)=-1,
解得:x=-$\frac{7}{4}$,
经检验:x=-$\frac{7}{4}$是原方程的根,
∴原方程的解为:x=-$\frac{7}{4}$;
(2)两边同乘(x+2)(x-2),
得:(x-2)2-16=x2-1,
解这个方程得:x=-2,
经检验:x=-2是增根,方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
16.甲、乙、丙、丁四位同学到木工厂参观时,木工师傅拿尺子要他们帮助检测一个窗框是否是矩形,他们各自做了如下检测,检测后,他们都说窗框是矩形,你认为正确的是( )
| A. | 甲量得窗框两组对边分别相等 | |
| B. | 乙量得窗框对角线相等 | |
| C. | 丙量得窗框的一组邻边相等 | |
| D. | 丁量得窗框的两组对边分别相等且两条对角线相等 |
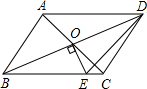 如图,?ABCD,对角线AC、BD交于点O,EO⊥BD于O交BC于E,若AB=5,△DEC的周长为13,则AD的长为8.
如图,?ABCD,对角线AC、BD交于点O,EO⊥BD于O交BC于E,若AB=5,△DEC的周长为13,则AD的长为8.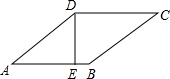 如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,$\frac{AE}{AD}=\frac{4}{5}$,下列结论:
如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,$\frac{AE}{AD}=\frac{4}{5}$,下列结论: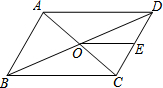 如图,已知?ABCD的对角线AC、BD相交于点O,点E是CD的中点,若BD=12cm,△DOE的周长为15cm,则?ABCD的周长为36cm.
如图,已知?ABCD的对角线AC、BD相交于点O,点E是CD的中点,若BD=12cm,△DOE的周长为15cm,则?ABCD的周长为36cm. 如图,边长为1的正方形网格在平面直角坐标系中,A(-1,3),B(3,-2).
如图,边长为1的正方形网格在平面直角坐标系中,A(-1,3),B(3,-2). 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字.请认真观察此图,写出(a+b)3的展开式(a+b)3=a3+3a2b+3ab2+b3.
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字.请认真观察此图,写出(a+b)3的展开式(a+b)3=a3+3a2b+3ab2+b3.