题目内容
13. 如图,边长为1的正方形网格在平面直角坐标系中,A(-1,3),B(3,-2).
如图,边长为1的正方形网格在平面直角坐标系中,A(-1,3),B(3,-2).(1)求△AOB的面积;
(2)设AB交x轴于点C,求点C的坐标.
分析 (1)根据S△AOB=S△ABD-S梯形ADEO-S△OBE即可求得;
(2)根据S△AOB=S△AOC+S△BOC=$\frac{1}{2}$•OC•3+$\frac{1}{2}$•OC•2=$\frac{1}{2}$•OC•5=3.5,从而求得OC的长,即可求得C点的坐标.
解答  解:(1)如图,S△AOB=S△ABD-S梯形ADEO-S△OBE=$\frac{1}{2}$×5×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$(2+5)×1=10-3-3.5=3.5.
解:(1)如图,S△AOB=S△ABD-S梯形ADEO-S△OBE=$\frac{1}{2}$×5×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$(2+5)×1=10-3-3.5=3.5.
(2)∵S△AOB=S△AOC+S△BOC=$\frac{1}{2}$•OC•3+$\frac{1}{2}$•OC•2=$\frac{1}{2}$•OC•5=3.5,
∴OC=1.4,
∴点C的坐标为(1.4,0).
点评 本题考查了三角形的面积的求法,分割法求三角形的面积是解题的关键.

练习册系列答案
相关题目
4. 如图,将一张长方形纸条折叠,如果∠1=130°,则∠2=( )
如图,将一张长方形纸条折叠,如果∠1=130°,则∠2=( )
 如图,将一张长方形纸条折叠,如果∠1=130°,则∠2=( )
如图,将一张长方形纸条折叠,如果∠1=130°,则∠2=( )| A. | 100° | B. | 130° | C. | 150° | D. | 80° |
8.在500个数据中,用适当的方法抽取50个为样本进行统计,频率分布表中54.5~57.5这一组的频率是0.15,那么估计总体数据在54.5~57.5之间的约有( )
| A. | 150个 | B. | 75个 | C. | 60个 | D. | 15个 |
18.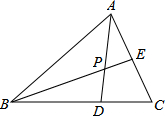 如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )
如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )
 如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )
如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )| A. | $\frac{1}{3}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{13}{20}$ |
5. 七巧板被西方人称为“东方魔板”.如图的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形的边长为8cm,则“一帆风顺”图中阴影部分的面积为( )
七巧板被西方人称为“东方魔板”.如图的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形的边长为8cm,则“一帆风顺”图中阴影部分的面积为( )
 七巧板被西方人称为“东方魔板”.如图的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形的边长为8cm,则“一帆风顺”图中阴影部分的面积为( )
七巧板被西方人称为“东方魔板”.如图的两幅图是由同一副七巧板拼成的.已知七巧板拼成的正方形的边长为8cm,则“一帆风顺”图中阴影部分的面积为( )| A. | 16cm2 | B. | 8cm2 | C. | 4cm2 | D. | 2cm2 |
 如图,在?ABCD中,对角线AC、BD相交成的锐角α为60°,若AC=10,BD=8,则?ABCD的面积是20$\sqrt{3}$.
如图,在?ABCD中,对角线AC、BD相交成的锐角α为60°,若AC=10,BD=8,则?ABCD的面积是20$\sqrt{3}$.