题目内容
10．（1）解不等式组：$\left\{\begin{array}{l}{x+4≤3（x+2）}\\{\frac{x-1}{2}＜\frac{x}{3}}\end{array}\right.$（2）解方程：$\frac{3x}{x+2}$-$\frac{2}{x-2}$=3．
分析 （1）先求出每一个不等式的解集，再求其公共解集即可；
（2）利用解分式方程的步骤与方法解答即可．
解答 （1）解：由（1）得，x≥-1，
由（2）得，x＜3，
不等式组的解集是-1≤x＜3；
（2）解：去分母，得3x（x-2）-2（x+2）=3（x+2）（x-2）
去括号，得3x2-6x-2x-4=3x2-12
整理，得-8x=-8
解得x=1
检验，当x=1时，（x+2）（x-2）≠0，
所以x=1是原方程的解．
点评 此题考查解不等式组与分式方程，掌握解不等式组与解分式方程的步骤与方法是解决问题的关键．
练习册系列答案
相关题目
18．
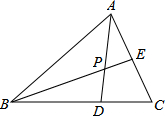如图，△ABC的面积为3，BD：DC=2：1，E是AC的中点，AD与BE相交于点P，那么四边形PDCE的面积为（ ）
如图，△ABC的面积为3，BD：DC=2：1，E是AC的中点，AD与BE相交于点P，那么四边形PDCE的面积为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{7}{10}$ | C． | $\frac{3}{5}$ | D． | $\frac{13}{20}$ |
5．
七巧板被西方人称为“东方魔板”．如图的两幅图是由同一副七巧板拼成的．已知七巧板拼成的正方形的边长为8cm，则“一帆风顺”图中阴影部分的面积为（ ）
七巧板被西方人称为“东方魔板”．如图的两幅图是由同一副七巧板拼成的．已知七巧板拼成的正方形的边长为8cm，则“一帆风顺”图中阴影部分的面积为（ ）| A． | 16cm2 | B． | 8cm2 | C． | 4cm2 | D． | 2cm2 |
如图，△ABC中，DE∥BC，分别交BA，CA的延长线于D、E，EF∥CD交AB于F，求证：AD2=AF•AB．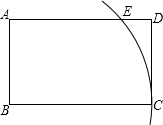
如图，在矩形ABCD中，$\frac{AB}{BC}=\frac{3}{5}$，以点B为圆心，BC长为半径画弧，交边AD于点E．若AE•ED=8，则矩形ABCD的面积为30．